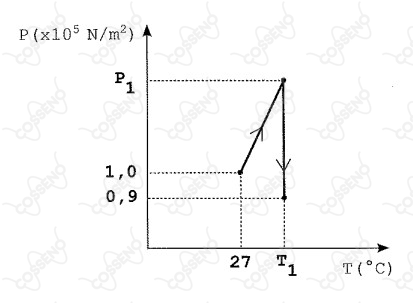
Um reservatório fechado contém certa quantidade de um gás ideal à pressão inicial . Num primeiro processo, esse gás é lentamente aquecido de até uma temperatura . Num o segundo processo, um pequeno orifício é aberto na parede do reservatório e, muito lentamente, deixa-se escapar do conteúdo inicial do gás mantendo-se, porém, a temperatura constante , ver gráfico). Sabendo que, ao final do segundo processo, a pressão do gás no interior do reservatório é , o valor de , em , é
CossenoGPT
Teste
gratuitamente agora
mesmo! 

(lembre-se que as equações de transformações gasosas ideais nascem da conservação da quantidade de matéria advinda da Equação de Clapeyron $PV=nRT$)
Como o reservatório está fechado na primeira transformação, é um processo isocórico:
$$\frac{10^5}{300}=\frac{P1}{T1}$$
Como há o vazamento de gás temos que:
$$\frac{3}{4}\frac{P1*V}{R*T1}=\frac{P2*V}{R*T2}$$
$$T2=T1=\frac{0,9*10^5*4*300}{3*10^5}$$
$$T1=360K$$
$$T1=87°C$$

