A esfera de massa tem o módulo da sua velocidade reduzida a zero
na colisão frontal e inelástica (ou parcialmente elástica) com a esfera
de massa . Por sua vez, a esfera de massa encontra-se
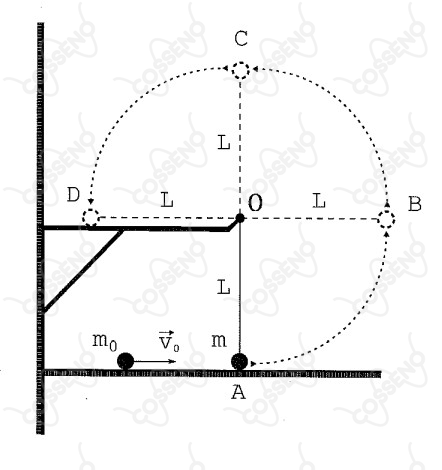
inicialmente em repouso na posição , suspensa por um fio inextensível
e de massa desprezível. Após a colisão, percorre a trajetória circular
de raio igual ao comprimento do fio. Despreze o atrito no pivô
e a resistência do ar. Para que a esfera de massa percorra a
trajetória circular, o valor mínimo do módulo da velocidade antes da
colisão, é
$g$ é a aceleração da gravidade.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Como não há a atuação de forças externas no sistema, podemos conservar a quantidade de movimento do sistema, e sabendo que a velocidade do corpo inicial é zero após a colisão:
$$moVo=2moV$$
$$Vo=2V$$
A condição crítica em que a esfera de $m$ tem que passar é a do topo do Looping e sua velocidade nesse ponto deve ser a mínima possível.
Conservando a energia mecânica do chão até o topo:
$$\frac{mV²}{2}=mg2L + \frac{mV'}{2}$$
Resultante centrípeta no topo do Looping:
$$\frac{mV'^2}{L}=mg$$
Substituindo:
$$V²=4gL + gL$$
Dessa forma:
$$Vo=2\sqrt{5gL}$$

