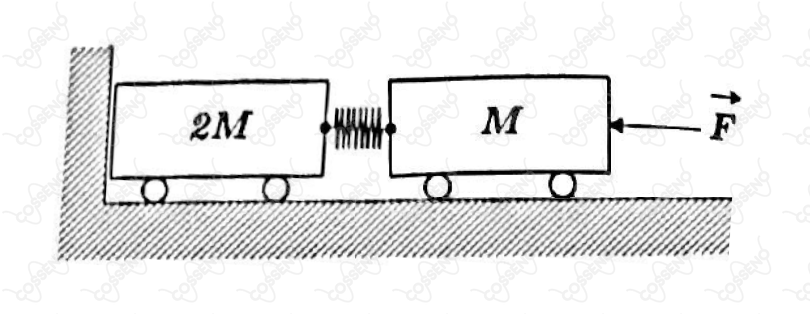
No laboratório de mecânica, carrinhos de massa e são unidos por uma mola elástica ideal e oscilam livremente em um plano liso com período . A seguir, o sistema é comprimido contra uma parede por uma força F atuando sobre a massa , conforme ilustra a figura abaixo. Nessa situação, a mola é sujeita a uma compressão com respeito ao seu comprimento natural. Em um determinado instante, a massa M é liberada e o sistema entra em movimento. Assinale a alternativa que contém a máxima velocidade atingida pelo centro de massa no movimento subsequente.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

i) Massa reduzida no sistema isolado: $\mu = \frac{m1.m2}{m1 + m2} = \frac{2M.M}{2M +M} = \frac{2M}{3}$
Período de oscilação: $T = 2\pi\sqrt{\frac{\mu}{k}} =2\pi\sqrt{\frac{2M}{3k}}$
ii) A velocidade máxima do centro de massa vai ocorrer quando não haver mais impulso gerado por forças externas.
iii) Conservação da energia mecânica:
$\frac{1}{2}kl^2 = \frac{1}{2}Mv^2 \therefore v = \sqrt{\frac{k}{m}}l$
Velocidade do centro de massa:
$v_{máx} = \frac{m1.v1 +m2.v2}{m1 + m2} = \frac{2M.0 +M.v}{3M} = \frac{1}{3}v \therefore v_{máx} = \frac{1}{3}\sqrt{\frac{k}{m}}l$
$\sqrt{\frac{k}{M}} = \frac{2\pi}{T}.\sqrt{\frac{2}{3}} \therefore v_{máx} = \sqrt{\frac{8}{27}}.\frac{\pi.l}{T}$

