A priori, podemos relembrar sobre o teorema da raiz complexa conjugada de um polinômio, o qual diz: Se um número complexo $ a +b\mathcal{i}$ , com $b \neq 0$ e $\mathcal{i}$ sendo a unidade imaginária, é raiz de um polinômio, então, o conjugado desse mesmo número, $ a -b\mathcal{i} $, também é raiz desse mesmo polinômio Assim, como $ \mathcal{i}$ é raiz do polinômio $P(\mathcal{z})$, $-\mathcal{i}$ também será raiz de $P(\mathcal{z})$. Portanto, usando o teorema da decomposição dos polinômios, podemos escrever $ P(\mathcal{z})$ da seguinte forma:$$ P(\mathcal{z}) = (\mathcal{z} - \mathcal{i})(\mathcal{z} + \mathcal{i})(\mathcal{z} - \mathcal{r}3)(\mathcal{z} - \mathcal{r}4)$$ $P(\mathcal{z}) = (\mathcal{z}^2 + 1)(\mathcal{z} - \mathcal{r}3)(\mathcal{z} - \mathcal{r}4)$ Em que $\mathcal{r}3$ e $\mathcal{r}4$ são as outras duas raízes de $P(\mathcal{z})$. A fatoração acima implica que, ao dividirmos $P(\mathcal{z})$ por $( \mathcal{z}^2 + 1)$, teremos um polinômio $Q(\mathcal{z}) $, de tal forma que suas raízes serão: $\mathcal{r}3$ e $\mathcal{r}4$. Realizando a divisão das expressões, temos: $$ \frac{ \mathcal{z}^4 - 6 \mathcal{z}^3 + 14 \mathcal{z}^2 - 6 \mathcal{z} + 13} { \mathcal{z}^2 + 1} = \mathcal{z}^2 - 6 \mathcal{z} + 13$$ Agora sabemos muito bem o que fazer. Usando Bhaskara na equação acima, temos: $$ \frac{ 6 \pm \sqrt{ 36 - 52}} { 2} = \frac{6 \pm \sqrt{-16}}{2} = \frac{ 6 \pm 4\mathcal{i}}{2} = 3 \pm 2\mathcal{i}$$ Assim: $\mathcal{r}3 = 3 + 2\mathcal{i}$ e $\mathcal{r}4 = 3 - 2\mathcal{i}$. Enfim, distribuindo todas as raízes no plano de Argand-Gauss, podemos perceber que o quadrilátero formado é um trapézio: 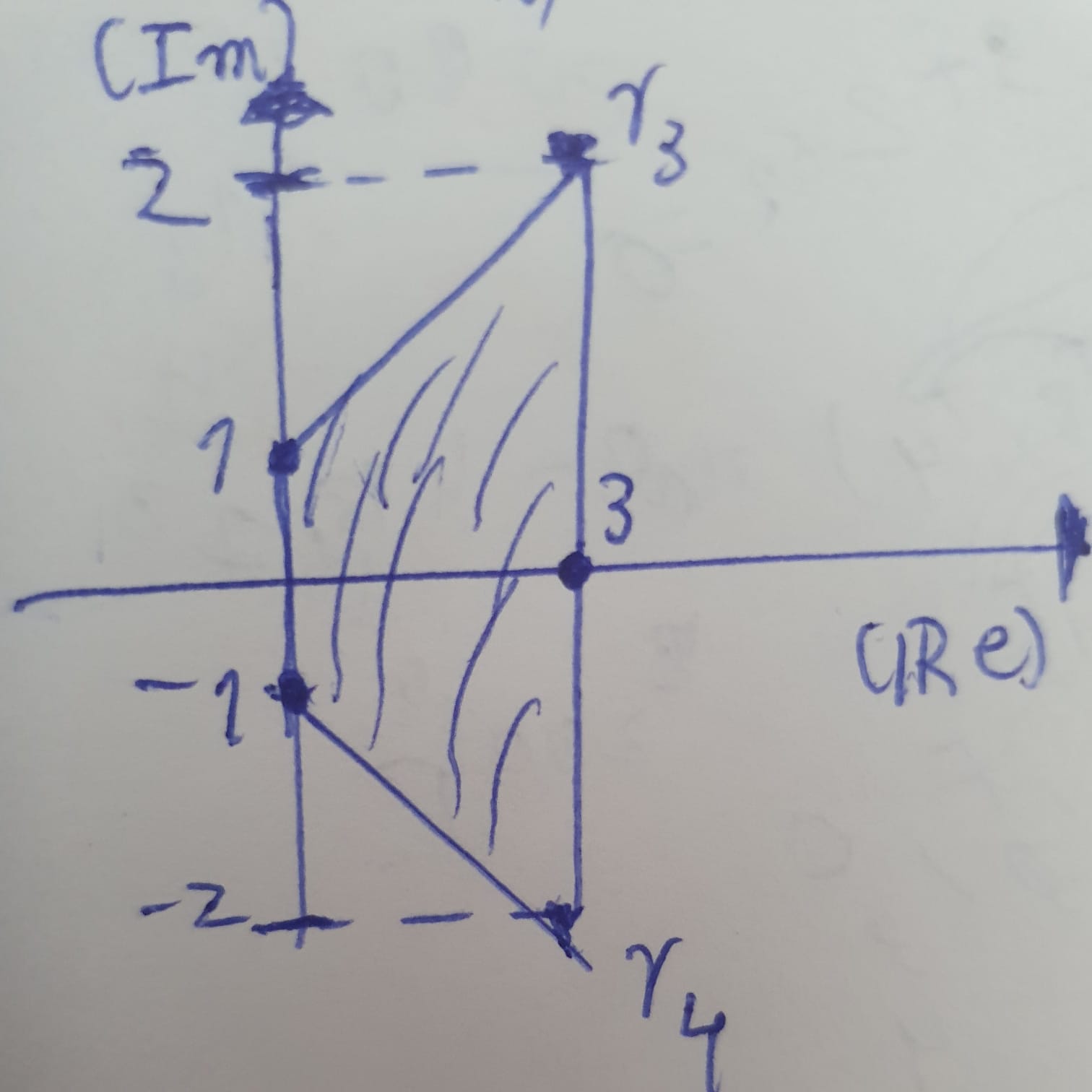Ao observar a imagem, temos que sua altura, base menor e base maior valem, respectivamente, 3, 2 e 4. Assim, a área do quadrilátero será:$$ \frac{(2+4) 3}{2} = \frac {18}{2} = 9$$ Assim, finalmente concluímos que a alternativa correta será a alternativa: LETRA D)