Sobre uma prancha horizontal de massa desprezível e apoiada no centro, dois discos, de massas e , respectivamente, rolam com as respectivas velocidades e , constantes, em direção ao centro, do qual distam e , conforme a figura.
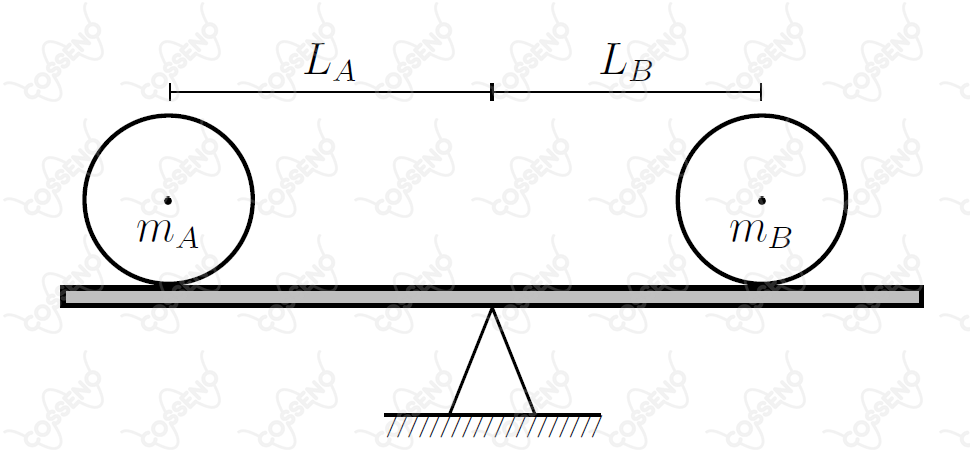
Com o sistema em equilíbrio antes que os discos colidam, a razão é dada por
CossenoGPT
Teste
gratuitamente agora
mesmo! 

i) $\Sigma M = 0 \therefore mA.g.La = mB.g.Lb \Rightarrow mA.La = mB.Lb$
ii) considerando que a esfera A ande $\Delta{Sa}$ e a esfera B ande $\Delta{Sb}$, teremos:
$mA.g.(La - \Delta{Sa}) = mB.g.(\Delta{Lb - Sb}) \therefore $
$mA.La - mA.\Delta{Sa} = mB.Lb - mb.\Delta{Sb} \therefore$
$mA.vA = mB.vB \therefore {\frac{vA}{vB} = \frac{mB}{mA}}$

