Em equilíbrio, o tubo emborcado da figura contém mercúrio e ar aprisionado. Com a pressão atmosférica de de a uma temperatura de , a altura da coluna de mercúrio é de .
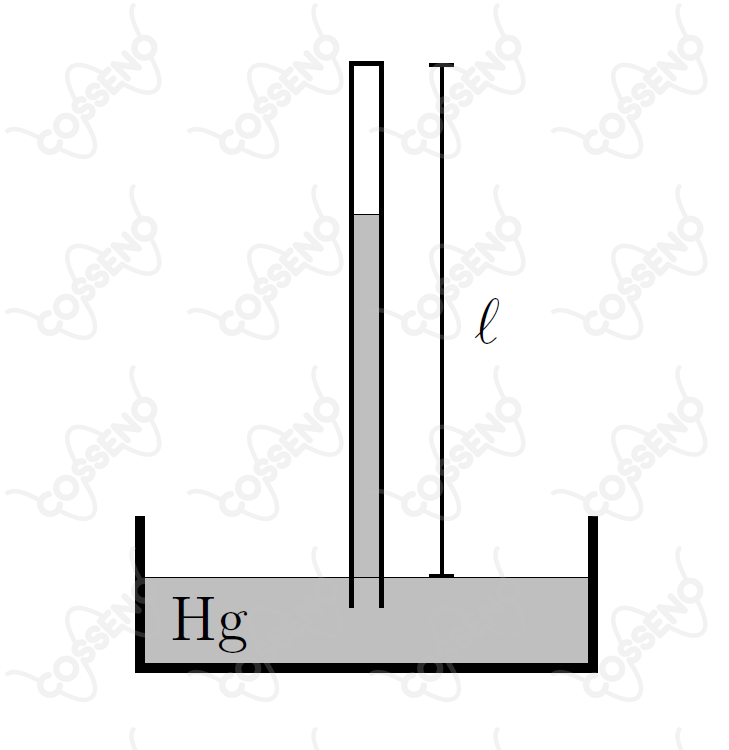
Se a pressão atmosférica cai a de a uma temperatura de , a coluna de mercúrio é de . Determine o comprimento aparente do tubo.
Massa específica do mercúrio: $13{,}6\ g/cm^3$
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A questão faz alusão a um dos experimentos mais afamados da hidrostática: o barômetro de Torricelli. Nele, o enunciado nos informa duas situações distintas, assim como nos é solicitado o comprimento aparente do tubo. A análise dos dois momentos não é complicada, basicamente, deve-se conhecer a $\text{Lei de Stevin}$; dela, sabemos que devido o sistema estar em equilíbrio é possível traçar uma linha isobárica, esta que nos auxiliará a encontrar a pressão na coluna de ar - visto que ele já nos dá a da coluna de mercúrio, tal-qualmente a pressão atmosférica. Vejamos cada caso,
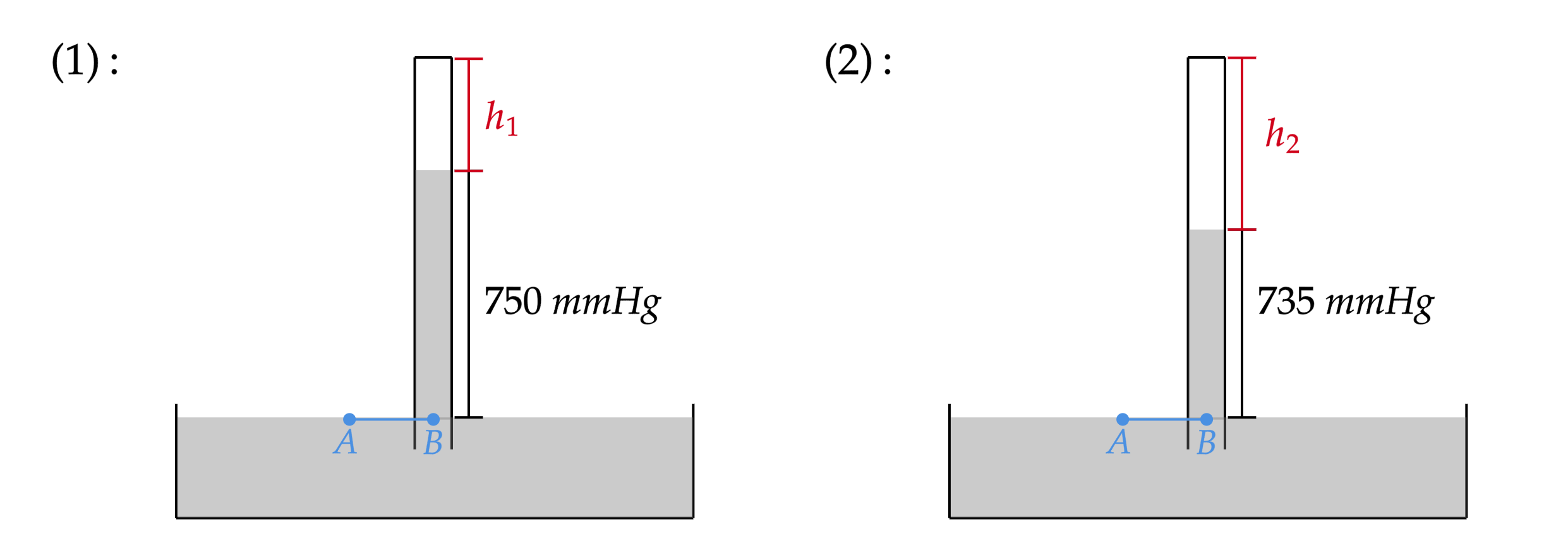 Com isso, sabdio que $P_A = P_B$, pode-se escrever:\begin{matrix}
(1): & P_{h_1} = P_{ar_1} - P_{coluna_1} = 760 - 750 &\therefore& P_{h_1} = 10 \ \pu{mmHg} \\
(2): & P_{h_2} = P_{ar_2} - P_{coluna_2} = 740 - 735 &\therefore& P_{h_2} = 5\phantom{0} \ \pu{mmHg}
\end{matrix}Veja que já sabemos a pressão exercida pela camada de ar do tubo em ambos os casos, logo, é possível descobrir a relação entre as alturas $h_1$ e $h_2$. Vale ressaltar que devemos admitir a idealidade dos ar em questão, assim, pela equação geral dos gases ideais:\begin{matrix}
\dfrac{P_{h_1} V_1}{T_1} = \dfrac{P_{h_2} V_2}{T_2} &,& V_1 = S\cdot h_1 &\wedge& V_2 = S\cdot h_2
\end{matrix}$\color{#ff1729}{\text{Obs:}}$ Estamos assumindo que a área da seção transversal $S$ do tubo permanece constante durante os dois eventos, o que é bem plausível ao admitir que o tubo seja fino (inclusive, ele deve ser), assim como a baixa variação de temperatura. Além disso, não estamos contabilizando a eventual pressão de vapor do mercúrio - o que tornaria a análise incabível.
Substituindo os valores fornecidos na relação, tem-se:\begin{matrix}
\dfrac{10(Sh_1)}{300} = \dfrac{5 (S h_2)}{275} &\therefore& 11h_1 = 6h_2
\end{matrix}Pois bem, agora já possuímos um sistema com três equações e três incógnitas, veja:\begin{cases} \ \ \ ℓ \ \ \ = 750 + h_1 \\ \ \ \ ℓ \ \ \ = 735 + h_2 \\ 11h_1 = 6h_2
\end{cases}Multiplicando a primeira linha por $11$ e a segunda linha $6$ e, assim, subtraindo a segunda na primeira, constata-se:\begin{matrix}
11 ℓ - 6 ℓ =11(750) - 6(735)
\end{matrix}Portanto,\begin{matrix} {ℓ = 768} \ \pu{mm} & \tiny{\blacksquare}
\end{matrix}
Com isso, sabdio que $P_A = P_B$, pode-se escrever:\begin{matrix}
(1): & P_{h_1} = P_{ar_1} - P_{coluna_1} = 760 - 750 &\therefore& P_{h_1} = 10 \ \pu{mmHg} \\
(2): & P_{h_2} = P_{ar_2} - P_{coluna_2} = 740 - 735 &\therefore& P_{h_2} = 5\phantom{0} \ \pu{mmHg}
\end{matrix}Veja que já sabemos a pressão exercida pela camada de ar do tubo em ambos os casos, logo, é possível descobrir a relação entre as alturas $h_1$ e $h_2$. Vale ressaltar que devemos admitir a idealidade dos ar em questão, assim, pela equação geral dos gases ideais:\begin{matrix}
\dfrac{P_{h_1} V_1}{T_1} = \dfrac{P_{h_2} V_2}{T_2} &,& V_1 = S\cdot h_1 &\wedge& V_2 = S\cdot h_2
\end{matrix}$\color{#ff1729}{\text{Obs:}}$ Estamos assumindo que a área da seção transversal $S$ do tubo permanece constante durante os dois eventos, o que é bem plausível ao admitir que o tubo seja fino (inclusive, ele deve ser), assim como a baixa variação de temperatura. Além disso, não estamos contabilizando a eventual pressão de vapor do mercúrio - o que tornaria a análise incabível.
Substituindo os valores fornecidos na relação, tem-se:\begin{matrix}
\dfrac{10(Sh_1)}{300} = \dfrac{5 (S h_2)}{275} &\therefore& 11h_1 = 6h_2
\end{matrix}Pois bem, agora já possuímos um sistema com três equações e três incógnitas, veja:\begin{cases} \ \ \ ℓ \ \ \ = 750 + h_1 \\ \ \ \ ℓ \ \ \ = 735 + h_2 \\ 11h_1 = 6h_2
\end{cases}Multiplicando a primeira linha por $11$ e a segunda linha $6$ e, assim, subtraindo a segunda na primeira, constata-se:\begin{matrix}
11 ℓ - 6 ℓ =11(750) - 6(735)
\end{matrix}Portanto,\begin{matrix} {ℓ = 768} \ \pu{mm} & \tiny{\blacksquare}
\end{matrix}

Ampliar Imagem

