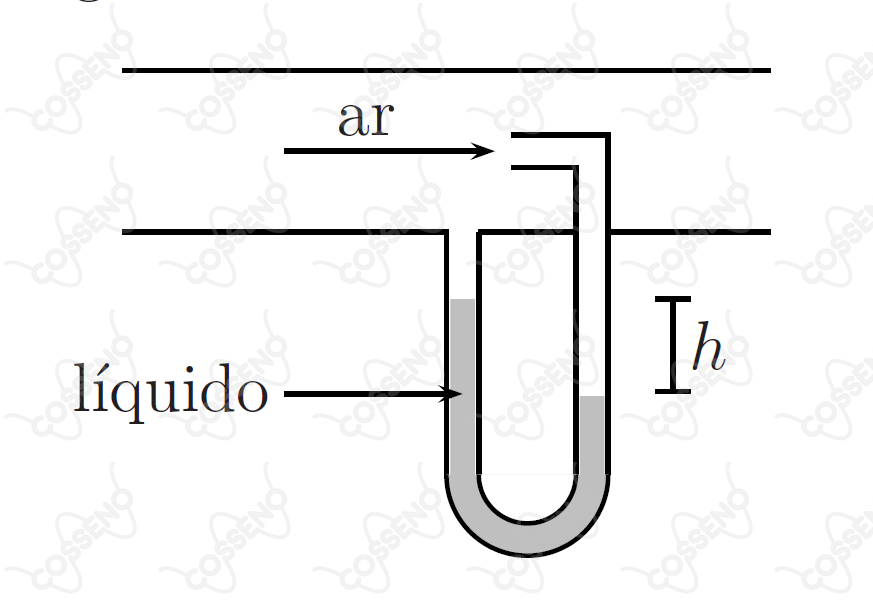
Um estudante usa um tubo de Pitot esquematizado na figura para medir a velocidade do ar em um túnel de vento.
A densidade do ar é igual a e a densidade do líquido é , sendo . Nessas condições a velocidade do ar é aproximadamente igual a
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Esta resolução é a primeira a ser publicada no Cosseno Respostas, para demonstrar o funcionamento do sistema. Escolhemos uma questão de hidrodinâmica bem simples, aproveitando a oportunidade para explicar como funciona o tubo de Pitot.
A figura mostra o ar em movimento por um tubo aberto, com velocidade $v$ desconhecida, onde se encontra uma das extremidades do tubo de Pitot. Para facilitar a análise da questão, vamos dar nomes a pontos importantes da figura.
- Seja $A$ o ponto logo antes da entrada da extremidade superior do tubo.
- Seja $B$ o ponto que se encontra na extremidade direita do tubo, na interface entre o ar e o líquido
- Seja $C$ o ponto que se encontra na extremidade esquerda do tubo, na interface entre o ar e o líquido
A aproximação mais comum é assumir que na entrada no tubo de Pitot (após o ponto $A$), a velocidade do ar é igual a ZERO. Cuidado! Muitos materiais online e cursinhos incorretamente assumem que a velocidade do ar ao longo do tubo é igual a $v\ne0$, o que é incorreto. No entanto, mesmo assumindo que a velocidade do ar próximo ao ponto $B$ é igual a $v$, é obtida a resposta certa em questões objetivas (o famoso acochambrar). Já veremos o motivo.
Escrevendo a equação de Bernoulli para os pontos $A$ e $B$: $$P_A + \rho_{Ar}\cdot g\cdot h_A + \frac{\rho_{Ar}v^2_{A}}{2} = P_B + \rho_{Ar}\cdot g\cdot h_B + \frac{\rho_{Ar}v^2_{B}}{2}$$Com $v_B=0$, podemos encontrar a diferença da pressão estática entre $B$ e $A$: $$P_B - P_A = \frac{\rho_{Ar}v^2_A}{2} + \rho_{Ar}g(h_A-h_B)$$
Considerando a baixa densidade do ar, a pressão causada pela coluna de ar sobre $B$ é desprezada em relação à pressão causada pelo movimento do ar. Em outras palavras, assumimos que é a pressão dinâmica do ar que impõe o desnível no líquido. Então, $$P_B - P_A = \frac{\rho_{Ar}v^2_A}{2}\quad(i)$$
Já para o líquido, entre os pontos $B$ e $C$: $$P_B + \rho_{L}\cdot g\cdot h_B + \frac{\rho_{L}v^2_{B}}{2} = P_C + \rho_{L}\cdot g\cdot h_C + \frac{\rho_{L}v^2_{C}}{2}\\P_B-P_C=g\rho_{L}(h_C-h_B)\quad(ii)$$
E assim, como $A$ e $C$ estão expostos ao ar do tubo (cuja pressão hidrostática é ignorada), podemos afirmar que pressão estática é igual nos dois pontos: $P_A=P_C$. Assim, podemos subtrair as equações obtidas anteriormente: $$(i)-(ii)\Rightarrow P_B-P_B=\frac{\rho_{Ar}v^2_A}{2}-g\rho_{L}(h_C-h_B)\\\rho_{L}\cdot gh=\frac{\rho_{Ar}v^2}{2}$$Note que podemos evidenciar aqui um conceito que já havíamos constatado anteriormente: é a pressão dinâmica do ar que impõe o desnível no líquido! Então, para uma resolução rápida e correta fisicamente, bastaria igualar: $$P_{\text{coluna líquido}} = P_{\text{dinâmica ar}}\\\rho_{L}\cdot gh=\frac{\rho_{Ar}v^2}{2}\\\boxed{v=\sqrt{2gh\frac{\rho_{L}}{\rho_{Ar}}}}$$Substituindo os valores dados no enunciado: $\displaystyle v=\sqrt{2\cdot 10\cdot 0{,}1\frac{12000}{1{,}2}}=100\sqrt{2}\simeq 1{,}4\cdot 10^2\ m/s$
Seja $A$ um ponto de entrada da extremidade superior do tubo de Pitot , $B$ um ponto pertencente a linha de corrente que contém o ponto $A$ (sendo $B \neq A$) , $C$ um ponto que pertence a interface entre o ar e o líquido na parte direita do tubo e $D$ um ponto que pertence a linha isobárica que contém $C$ e que está contido no líquido(Adote $y$ a sua distância vertical ao ponto $A$ e $B$).
Pela equação de Bernoulli podemos escrever que :
$P_{A} + \dfrac{\rho_{ar}v_{A}^2}{2} + \rho g h_{A} =P_{B} + \dfrac{\rho_{ar}v_{B}^2}{2} + \rho g h_{B} $
Tem-se que $h_{A} = h_{B}$ e a consideração que $v_{A} = 0$ , portanto
$P_{A} = P_{B} + \dfrac{\rho_{ar}v_{B}^2}{2} \implies v_{B} = \sqrt{\dfrac{2(P_{A} - P_{B})}{\rho_{ar}}}$
Note que $P_{C} = P_{D}$ , $P_{C} = P_{A} +\rho_{ar}g(y + h) $ e que $P_{D} = P_{B} +\rho_{ar}gy + \rho_{f}gh$
$\therefore$
$ P_{A} +\rho_{ar}g(y + h) =P_{B} +\rho_{ar}gy + \rho_{f}gh $
$\implies P_{A} + \rho_{ar}gh= P_{B} +\rho_{f}gh \implies P_{A} - P_{B} = hg(\rho_{f} - \rho_{ar})$
$\therefore$
$ v_{B} = \sqrt{\dfrac{2(P_{A} - P_{B})}{\rho_{ar}}} = v_{B} = \sqrt{\dfrac{2(P_{A} - P_{B})}{\rho_{ar}}}= v_{B} = \sqrt{\dfrac{2gh(\rho_{f} -\rho_{ar})}{\rho_{ar}}}$
$\rho_{ar}$ é desprezível em relação a $\rho_{f}$ , podemos escrever dessa forma que
$ v_{B} = \sqrt{\dfrac{2gh \cdot \rho_{f}}{\rho_{ar}}}$
Note que $v_{B}$ é a velocidade do ar $v_{ar}$, logo
$v_{ar} = \sqrt{\dfrac{2gh \cdot \rho_{f}}{\rho_{ar}}}$
Substituindo os valores no $SI$ para o caso da questão temos que :
$v_{ar} = \sqrt{\dfrac{2 \cdot 10 \cdot 0,1 \cdot 1,2 \cdot 10^4}{1,2}} $
$= v_{ar} = 10^2\sqrt{2} = \boxed{v_{ar} \approx 1,4 \cdot 10^2 \text{ m}/\text{s}}$
$\textbf{Resposta : Alternativa C}$


