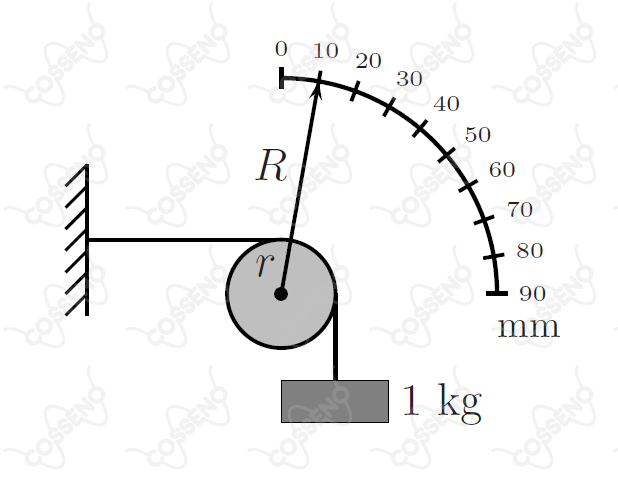
A figura mostra um dispositivo para medir o módulo de elasticidade (módulo de Young) de um fio metálico. Ele é definido como a razão entre a força por unidade de área da seção transversal do fio necessária para esticá-lo e o resultante alongamento deste por unidade de seu comprimento. Neste particular experimento, um fio homogêneo de de comprimento e de diâmetro, fixado numa extremidade, é disposto horizontalmente e preso pela outra ponta ao topo de uma polia de raio . Um outro fio preso neste mesmo ponto, envolvendo parte da polia, sustenta uma massa de . Solidário ao eixo da polia, um ponteiro de raio acusa uma leitura de na escala semicircular iniciada em zero.
Nestas condições, o módulo de elasticidade do fio é de
CossenoGPT
Teste
gratuitamente agora
mesmo! 

- A seção transversal de área $A$ do fio tem $0,2~\text{mm}$ de diâmetro, que corresponde a $0,1~\text{mm} = 10^{-4}~\text{m}$ de raio, isto é, uma seção de área $A = \pi \cdot 10^{-8} ~~\text{m}^2$ .
- A força $F$ sustentada pelo fio é o peso do bloco, ou seja, $F = 10~\text{N}$, considerando $g = 10~\text{m/s}^2$ .
Assim, a força por unidade de área da seção transversal do fio necessária para esticá-lo é$$\frac{F}{A} = \frac{10}{\pi \cdot 10^{-8}} = \frac{10^9}{\pi}~\text{N/m}^2$$
Ademais, se o alongamento do fio, a $R = 10r$, foi de $10~\text{mm} = 10^{-2}~\text{m}$, então o alongamento em relação a $r$ foi de $1~\text{mm} = 10^{-3}~\text{m}$, visto que o comprimento do arco é diretamente proporcional ao raio considerado. Assim, o resultante alongamento do fio por unidade de seu comprimento é a razão $\Large{\frac{10^{-3}~\text{m}}{1~\text{m}}}$$~= 10^{-3}$ .
Portanto, o módulo de elasticidade do fio é de$$\frac{\frac{F}{A}}{10^{-3}} = \frac{\frac{10^9}{\pi}~\text{N/m}^2}{10^{-3}} = \boxed{\frac{10^{12}}{\pi}~\text{N/m}^2}$$
$$\text{Alternativa } \mathbb{(A)}$$

