Uma massa suspensa por uma mola elástica hipotética, de constante de mola e comprimento , descreve um movimento oscilatório de frequência angular quando ela é deslocada para uma posição , abaixo de sua posição de equilíbrio em , e solta em seguida.
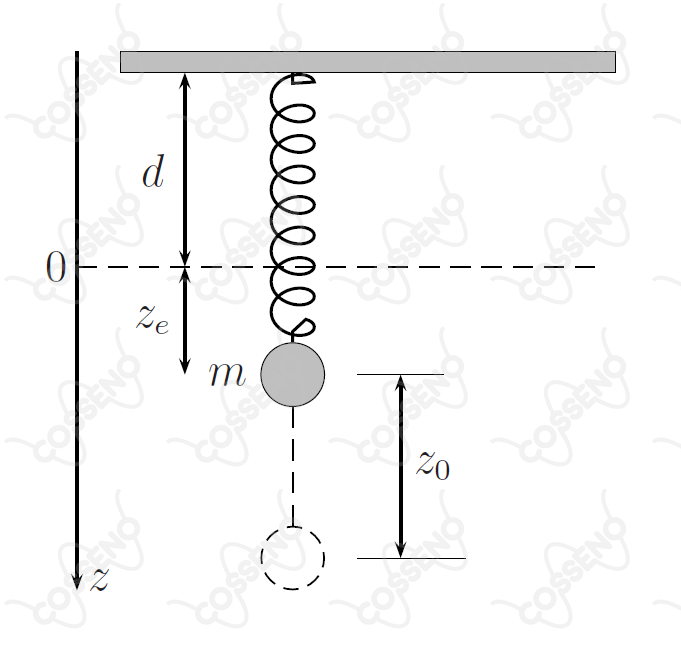
Considerando nula a força da mola para , determine o período de oscilação da massa e os valores de entre os quais a mesma oscila.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Com conhecimento da posição de equilíbrio, pode-se começar escrevendo:\begin{matrix}
F_{peso} = F_{mola} &\therefore& mg = kz_e & \ce{(I)}
\end{matrix}Agora, analisando mais minuciosamente o enunciado, nota-se que a mola apresenta o comportamento de um elástico - estica, porém não comprime. Nesse sentido, existem dois momentos na questão; um em que existe $\text{MHS}$ para $z>0$, e outro perfazendo um lançamento vertical para $z<0$. A princípio, o enunciado solicita o período do movimento, então a estratégia é dividir em partes. Assim, comecemos pelo $\text{MHS}$, este que é sabido a posição de equilíbrio $z_e$, e também a amplitude $2z_e$, o que nos permite equacionar:\begin{matrix}
z(t) = 2z_e\cos{(\omega t)} + z_e
\end{matrix}Observe que o $\text{MHS}$ só existe até o corpo atingir $z(t) = 0$, então o tempo até chegar lá é:\begin{matrix}
2z_e\cos{(\omega t)} + z_e = 0 &\Rightarrow& \cos{(\omega t)} = -\dfrac{1}{2} &\therefore& \omega t = \dfrac{2\pi}{3}
\end{matrix}O enunciado informa o $\omega$, logo:\begin{matrix}
t = \dfrac{2\pi}{3} \sqrt{\dfrac{m}{k}} & \ce{(II)}
\end{matrix}Por outro lado, para o lançamento vertical, primeiro é necessário encontrar a velocidade que o corpo atinge em $z(t) = 0$. Para isso, tem-se a conservação da energia mecânica, então pensando nos pontos $z(t) = z$ e $z(t) = 0$:\begin{matrix}
\dfrac{k(3z_e)^2}{2} = mg(3z_e) + \dfrac{mv^2}{2}
\end{matrix}Substituindo $\ce{(I)}$ no resultado acima, não é difícil constatar:\begin{matrix} v = \sqrt{3gz_e} & \ce{(III)}
\end{matrix}Com isso, para o tempo de subida, e consequentemente o de descida, segue:\begin{matrix}
0 = v -gt_s &\rightarrow& t_s = \sqrt{ \dfrac{3z_3}{g}} &\therefore& t_s = \sqrt{ \dfrac{3m}{k}}
\end{matrix}Como resultado, para o período $T$ do movimento, têm-se:\begin{matrix}
T = 2t + 2t_2
\end{matrix}Portanto,\begin{matrix} T = \sqrt{ \dfrac{m}{k}} \left( \dfrac{4\pi}{3} + 2\sqrt{3}\right) &\tiny{\blacksquare}\end{matrix}Veja que ainda resta encontrar os valores que $z$ oscila, ou seja, encontrar os extremos do movimento. Notoriamente, o extremo positivo já conhecemos, isto é, $z_{máx} = 3z_e$. No entanto, resta-nos encontrar o extremo negativo, o que não é difícil caso se conheça a $\text{equação de Torricelli}$ - repare que o extremo negativo é a altura máxima que o corpo pode atingir no lançamento vertical, por isso:\begin{matrix}
0^2 = v^2 + 2gz_{mín} &\therefore& z_{mín} = -\dfrac{3z_e}{2}
\end{matrix}Consequentemente, $z$ oscila entre:\begin{matrix}-
\dfrac{3z_e}{2}\le z \le 3z_e
\end{matrix}O que pode se reescrever substituindo $\text{(I)}$:\begin{matrix}-
\dfrac{3mg}{2k}\le z \le \dfrac{3mg}{k}&\tiny{\blacksquare}
\end{matrix}

