Vamos desenhar a situação descrita no enunciado: 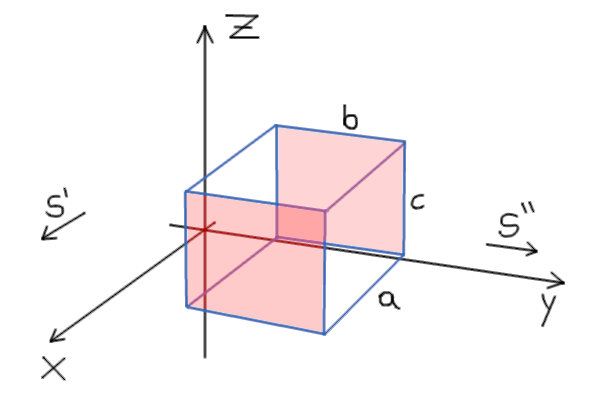As placas paralelas do capacitor, destacadas em vermelho, têm dimensões $b\times c$, enquanto a distância entre elas é $a$. Para comparar o campo elétrico nos referenciais indicados, precisamos de uma expressão que relacione $E$ com as dimensões indicadas na figura. Pode ser "tentador" usar a equação da diferença de potencial elétrico no capacitor $E = \frac{U}{a}$ e comparar o módulo do campo elétrico conforme $a$ varia, mas cuidado! O valor da diferença de potencial também depende de $E$, portanto não podemos considerá-la constante. Vamos usar outra expressão de $U$ e substituí-la na equação anterior para conseguirmos expressar o campo elétrico em uma equação que envolva apenas variáveis independentes de $E$. Assim, lembrando que $Q = CU$ e $C=\epsilon_0\dfrac{A}{a}$, podemos combinar essas equações para ficar com: $$U = \dfrac{Q}{\epsilon_0 A}$$ Substituindo a expressão acima em $E=\frac{U}{a}$ e, com base na figura, substituindo $A=b\times c$, encontramos a expressão do módulo do campo elétrico: $$E=\dfrac{Q}{\epsilon_0\cdot bc}$$ Essa expressão depende de $Q$ e $\epsilon_0$, que não variam conforme o referencial, e das dimensões $b$ e $c$, que podem sofrer contração dependendo da direção em que o referencial se movimenta. Note que não há dependência da dimensão $a$. Portanto, no referencial $S'$ o módulo campo elétrico também será: $$E'=\dfrac{Q}{\epsilon_0\cdot bc}$$ Já no referencial $S''$ haverá contração da dimensão $b$: $$b''=\dfrac{b}{\gamma}$$ Assim: $$E''=\gamma\cdot\dfrac{Q}{\epsilon_0\cdot bc}$$ Enfim, podemos calcular as razões pedidas no enunciado: $$\begin{cases}E'/E\quad=\quad1 \\ E''/E\quad=\quad\gamma\end{cases}\Longrightarrow\boxed{\text{Gab. C)}}$$