Podemos identificar que: 1) A partir da altura $AE$ podemos identificar dois triângulos semelhantes (vermelho e azul): $$\triangle ABC \sim \triangle ABE$$ E assim podemos relacionar os lados: $$\frac{\overline{AC}}{\overline{CE}} = \frac{\overline{BC}}{\overline{AC}}$$ 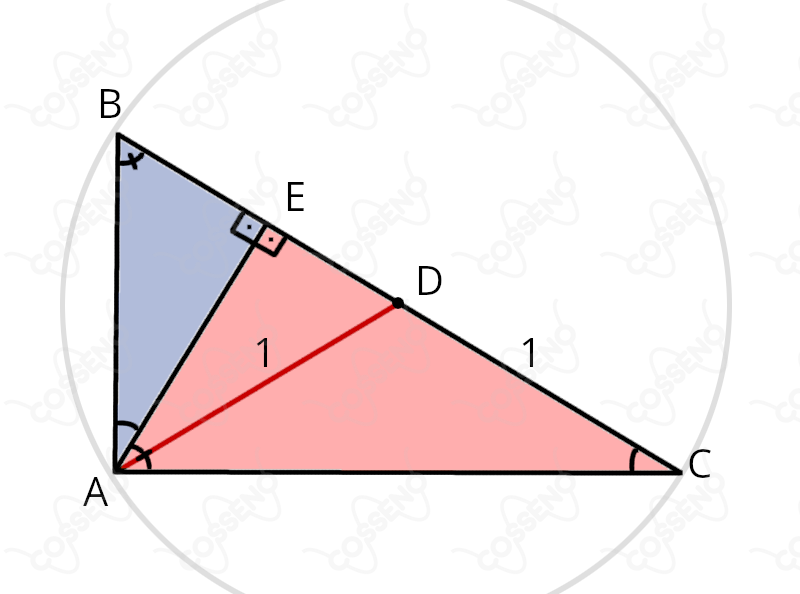2) Como o $\triangle ABC$ retângulo e $D$ é ponto médio da hipotenusa $BC$, então o circuncírculo centrado em $D$ terá raio igual à metade da hipotenusa: $$\overline{AD}=\overline{BD}=\overline{CD}=1$$ E assim podemos determinar $$\begin{align*}\overline{BE} &= \overline{BD} - \overline{DE}\\\sqrt{2}-1 &= 1 - \overline{DE}\\ \overline{DE} &= 2 - \sqrt{2}\ cm\end{align*}$$ E assim $$\begin{align*}\overline{CE} &= \overline{CD} + \overline{DE}\\ \overline{CE} &= 1 + (2-\sqrt{2})\\ \overline{CE} &= 3 - \sqrt{2}\end{align*}$$ Voltando à equação de semelhança: $$\frac{\overline{AC}}{3 - \sqrt{2}} = \frac{2}{\overline{AC}}$$ $$\overline{AC} = \sqrt{6-2\sqrt{2}}\quad\boxed{\text{Gab. C)}}$$