Um recipiente contém dois líquidos homogêneos e imiscíveis, e , com densidades respectivas e . Uma esfera sólida, maciça e homogênea, de massa , permanece em equilíbrio sob ação de uma mola de constante elástica , com metade de seu volume imerso em cada um dos líquidos, respectivamente, conforme a figura.
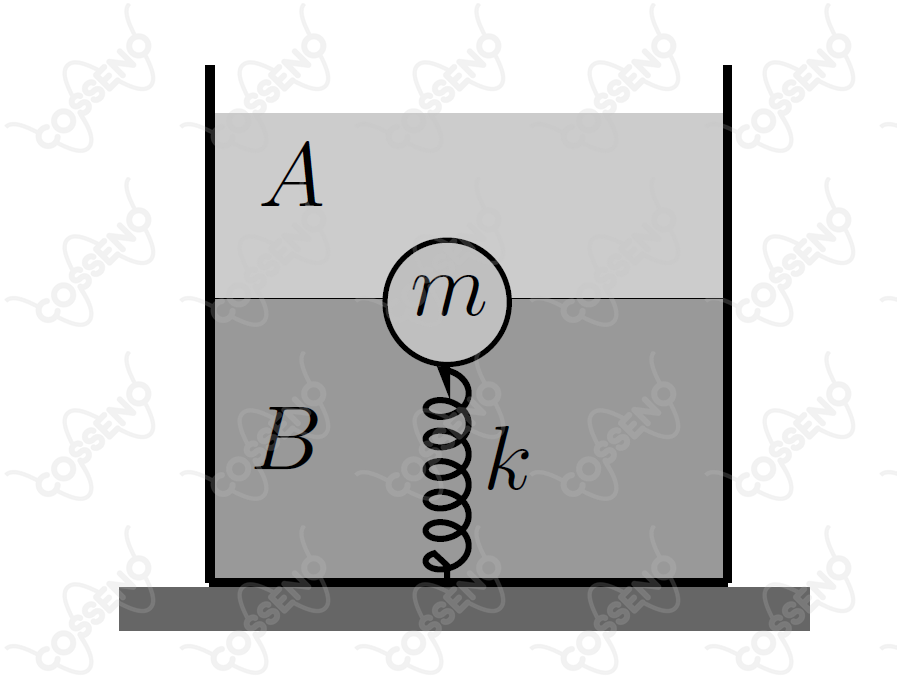
Sendo e , em que é a densidade da esfera, pode-se afirmar que a deformação da mola é de
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Equilíbrio das forças atuantes na esfera:$$E_A + E_B - T = P$$Em que $E_A$ e $E_B$ são, respectivamente, os empuxos produzidos pelos líquidos A e B, bem como $T$ e $P$ sendo, respectivamente, a tração exercida pela mola e o peso da esfera.
É importante reparar que, como as densidades dos dois líquidos são maiores que a da esfera, esta tende a subir, boiando na superfície do líquido A. Portanto, a mola exerce uma força contrária a essa tendência.
Sendo $V$ o volume da esfera, sabe-se que $V = \Large{\frac{5}{\rho}}\space$. Considerando, ademais, as informações do enunciado, temos:
$E_A = \frac{1}{2}\cdot \rho_A V g = 10g$ , $E_B = \frac{1}{2}\cdot \rho_B V g = 15g\space \space $ e $P = mg = 5g$ , assim:
$$10g+15g-T = 5g \implies T = 20g$$Considerando $T = 800\cdot d$ , em que $d$ é a deformação da mola, em metros, bem como $g = 10\space \text{m/s}^2$, conclui-se que:$$800\cdot d = 200 \implies \boxed{d = 1/4\space \text{m}}$$
$$\text{Alternativa } \mathbb{(D)}$$

