Comecemos por esboçar a situação descrita, 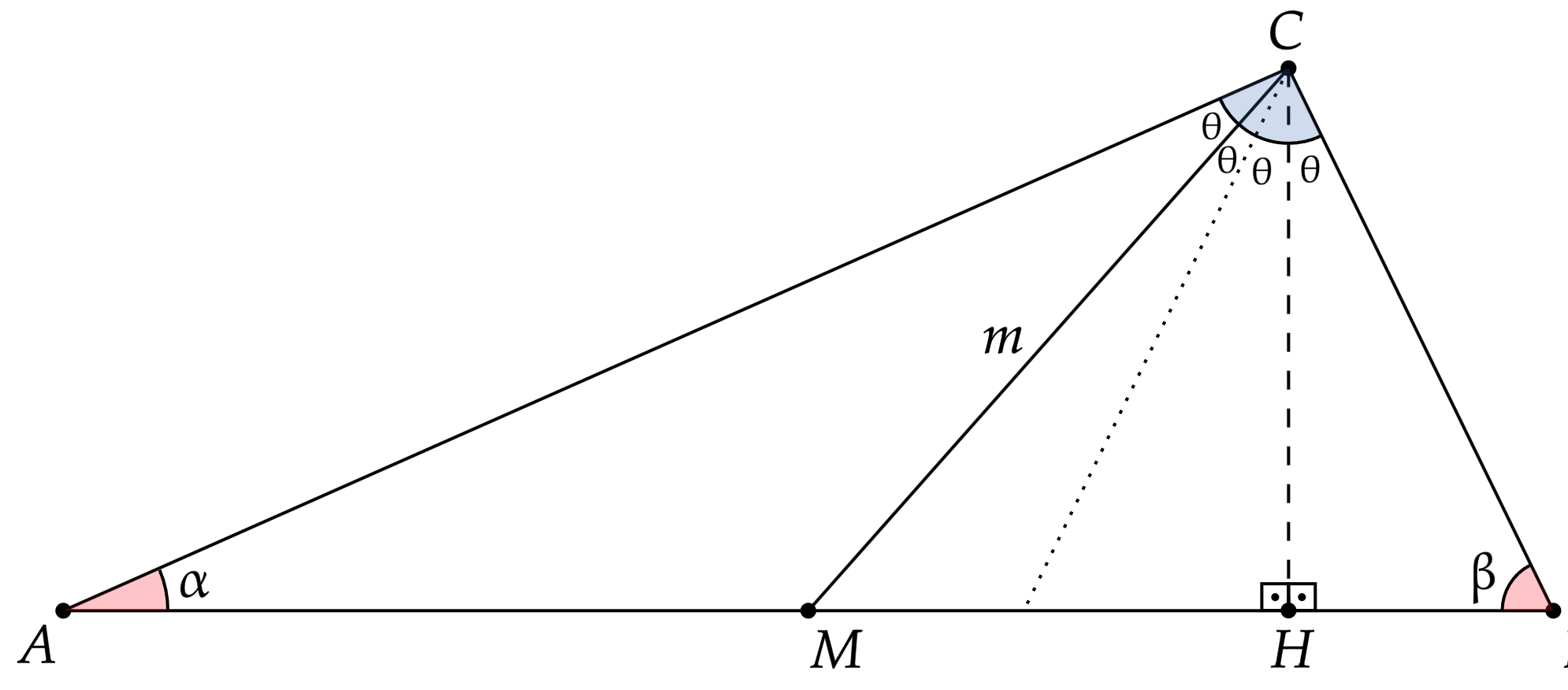Agora, nos interessa encontrar $m$, assim como todos os ângulos de $\Delta ABC$. Não é de interesse mais variáveis auxiliares, a cada nova variável há mais trabalho, mas por onde começar? Pois bem, possuímos alguns ângulos e lados de interesse, logo, tem-se a $\text{Lei dos Senos}$ como uma ferramenta útil. A ideia aqui é relacionar $m$ com $l$ e os ângulos destacados, então há dois triângulos notáveis:\begin{matrix} \Delta ACB: & \dfrac{m}{\sin{\alpha}} = \dfrac{l/2}{\sin{\theta}} \\ \\ \Delta BCM: & \dfrac{m}{\sin{\beta}} = \dfrac{l/2}{\sin{3\theta}} \end{matrix}$\color{#ff1729}{\text{Obs:}}$ $\overline{AM} = \overline{MB} = l/2 $ $• \ \text{b)}$ $\color{#3368b8}{ B\hat{A}C= \dfrac{\pi}{8} \ , \ A\hat{B}C= \dfrac{3\pi}{8} \ ,\ A\hat{C}B= \dfrac{\pi}{2}}$ Veja que é possível relacionar os ângulos a partir dos senos, isto é, segue:\begin{matrix}\text{(I)}:& \sin{\alpha} \sin{3\theta} = \sin{\beta}\sin{\theta} \end{matrix}Ora, já relacionamos os lados com os ângulos de interesse, então resta-nos verificar como os ângulos se relacionam. No caso, peguemos os triângulos $\Delta ACH$ e $\Delta BCH$, deles, têm-se:\begin{matrix}\text{(II)}:& \begin{cases} \alpha &+& 3\theta &=& \pi/2 \\ \beta&+& \theta&=& \pi/2 \end{cases}\end{matrix}Felizmente, tem-se ângulos complementares, ou seja, é possível reescrever $\text{(I)}$ como,\begin{matrix} \sin{\alpha}\cos{\alpha}= \sin{\beta}\cos{\beta} \end{matrix}Conhecido o arco-duplo da função seno,\begin{matrix} \sin{2\alpha} =\sin{2\beta} &\longrightarrow&\begin{cases} 2\alpha - 2\beta = 0 \\ 2\alpha + 2\beta = \pi \end{cases} \end{matrix}Pondere que $\alpha = \beta$ é inviável por $\text{(II)}$, o que implica uma única solução:\begin{matrix}\alpha + \beta = \pi/2 \end{matrix}Como resultado acima, constatamos três equações e três incógnitas para os ângulos de interesse, veja:\begin{matrix}\begin{cases} \alpha &+& 3\theta &=& \pi/2 \\ \beta&+& \theta&=& \pi/2 \\ \beta&+& \alpha&=& \pi/2 \end{cases} &\therefore& \alpha = \dfrac{\pi}{8} &\wedge& \beta= \dfrac{3\pi}{8} &\wedge& \theta= \dfrac{\pi}{8} \end{matrix}$• \ \text{a)}$ $\color{#3368b8}{m = l/2}$ Além disso, pela lei dos senos anteriormente utilizada, conclui-se:\begin{matrix} m = \left(\dfrac{\sin{\alpha}}{\sin{\theta}}\right) (l/2) &\therefore& m = \dfrac{l}{2} &\tiny{\blacksquare} \end{matrix}