No interior de um elevador encontra-se um tubo de vidro fino, em forma de U, contendo um líquido sob vácuo na extremidade vedada, sendo a outra conectada a um recipiente de volume com ar mantido à temperatura constante. Com o elevador em repouso, verifica-se uma altura de entre os níveis do líquido em ambos os braços do tubo. Com o elevador subindo com aceleração constante (ver figura), os níveis do líquido sofrem um deslocamento de altura de .
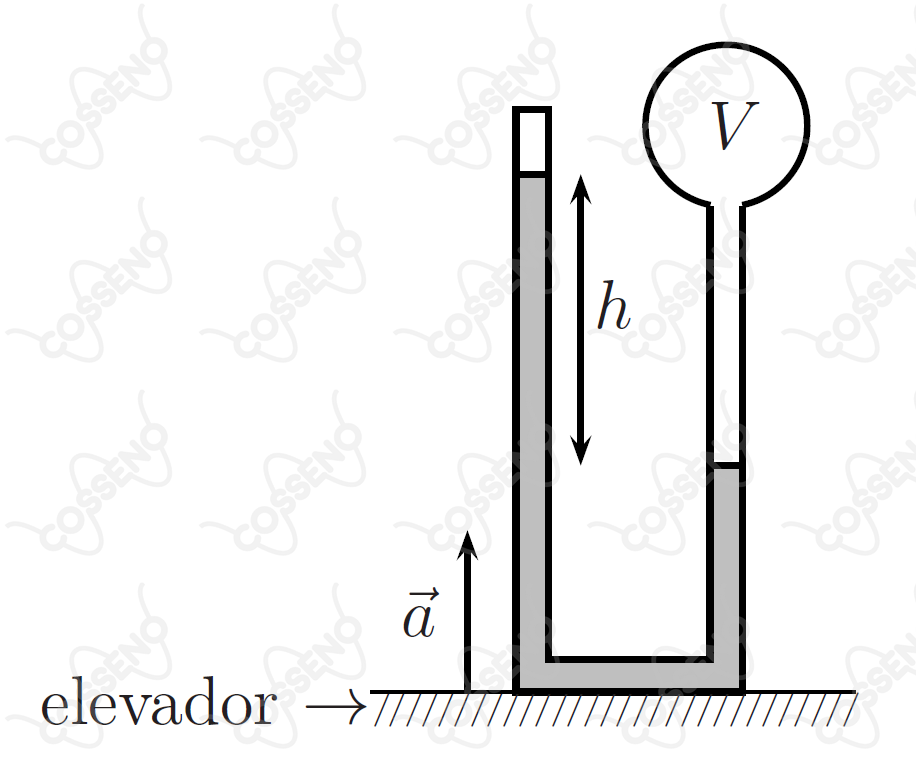
Pode-se dizer então que a aceleração do elevador é igual a
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Seja $d$ a densidade do líquido, $P_{ar}$ a pressão do ar e $g$ a aceleração da gravidade. Assim:$$\color{green}{10\cdot d\cdot g = P_{ar}}$$Pelo Princípio da Equivalência de Einstein, a situação do elevador acelerado, com módulo $a$ , é equivalente a estabelecer um campo gravitacional resultante de módulo $g+a$ , havendo, nesse sentido, uma maior pressão no ponto da superfície do líquido situado no tubo de extremidade vedada, produzindo, assim, uma coluna ascendente de $1\space \text{cm}$ do líquido no lado em que há o recipiente de volume $V$. A mudança de pressão do ar, no tubo, durante todo este processo é desprezível.
Como ascende $1\space \text{cm}$ num lado, descende $1\space \text{cm}$ no outro, desse modo, a nova altura da coluna será de $8 \space \text{cm}$ . Dessa forma:$$\color{green}{8\cdot d \cdot (g+a) = P_{ar}}$$
Das duas relações encontradas, a dividimos:$$\frac{10\cdot d\cdot g }{8\cdot d \cdot (g+a)} = \frac{P_{ar}}{P_{ar}} = 1 \implies 10\cdot g = 8\cdot (g+a)$$Tomando $g = 10\space \text{m/s}^2$, conclui-se que:$$2g = 8a \implies a = \frac{g}{4} = \frac{10}{4} = 2,5 \implies \boxed{a = 2,5\space \space \text{m/s}^2}$$
$$\text{Alternativa } \mathbb{(E)}$$

