Conforme a figura, um circuito elétrico dispõe de uma fonte de tensão de e de dois resistores, cada qual de .
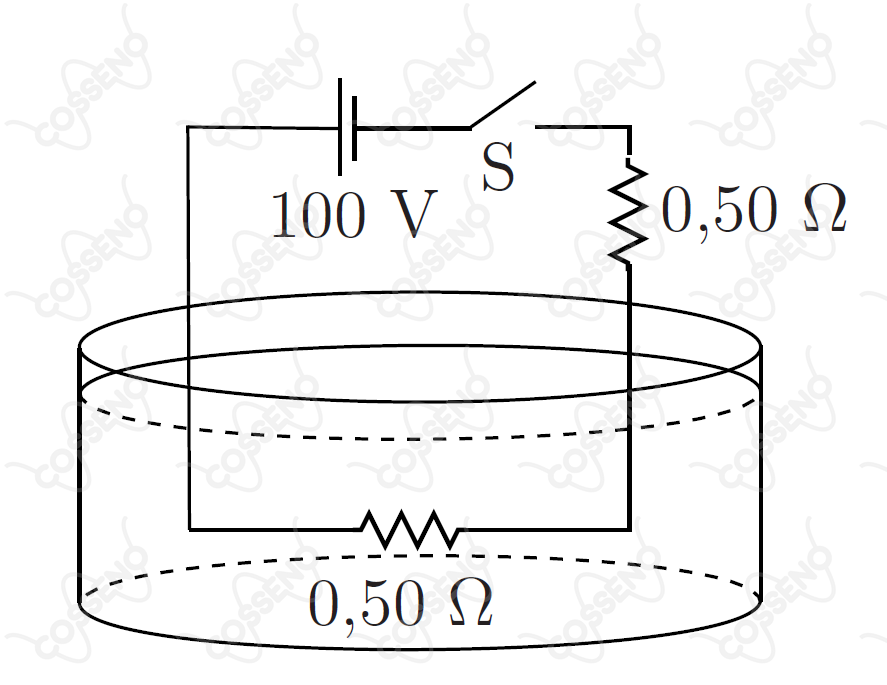
Um resistor encontra-se imerso no recipiente contendo de água com temperatura inicial de , calor específico e calor latente de vaporização . Com a chave S fechada, a corrente elétrica do circuito faz com que o resistor imerso dissipe calor, que é integralmente absorvido pela água. Durante o processo, o sistema é isolado termicamente e a temperatura da água permanece sempre homogênea. Mantido o resistor imerso durante todo o processo, o tempo necessário para vaporizar de água é
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Em tese, nota-se que a potência dissipada pelo resistor é a mesma absorvida pela água, ou seja:\begin{matrix}
Pot = R \cdot i^2 &,& Pot = \dfrac{Q}{\Delta t}
\end{matrix}Consequentemente, têm-se:\begin{matrix} \Delta t = \dfrac{Q}{R \cdot i^2} & \text{(I)}
\end{matrix}A resistência nos conhecemos pelo enunciado, agora, resta-nos achar a corrente assim como o calor necessário para o processo. Nesse sentido, comecemos pelo mais simples que é achar a corrente no sistema; conforme primeira lei de Ohm:\begin{matrix}
i = \dfrac{V}{2R} &\therefore& i =100 \ \pu{A}
\end{matrix}Por outro lado, para o calor do processo, pode-se começar com o princípio fundamental da termodinâmica:\begin{matrix}
Q = Q_{água} + Q_{vapor}
\end{matrix}Então,\begin{matrix}Q = 2\cdot (4,18 \cdot 10^3) \cdot (100-20) + 1\cdot (2230 \cdot 10^3)
\end{matrix}\begin{matrix}Q = 2898,8 \cdot 10^3 \ \pu{J}
\end{matrix}Portanto, substituindo os resultados acima em $ \text{(I)}$:\begin{matrix}
\Delta t = \dfrac{2898,8 \cdot 10^3 }{0,5 \cdot 100^2} \approx 580 \ \pu{s}
\end{matrix}\begin{matrix}Letra \ (E)
\end{matrix}

