No interior de um carrinho de massa mantido em repouso, uma mola de constante elástica encontra-se comprimida de uma distância , tendo uma extremidade presa e a outra conectada a um bloco de massa , conforme a figura.
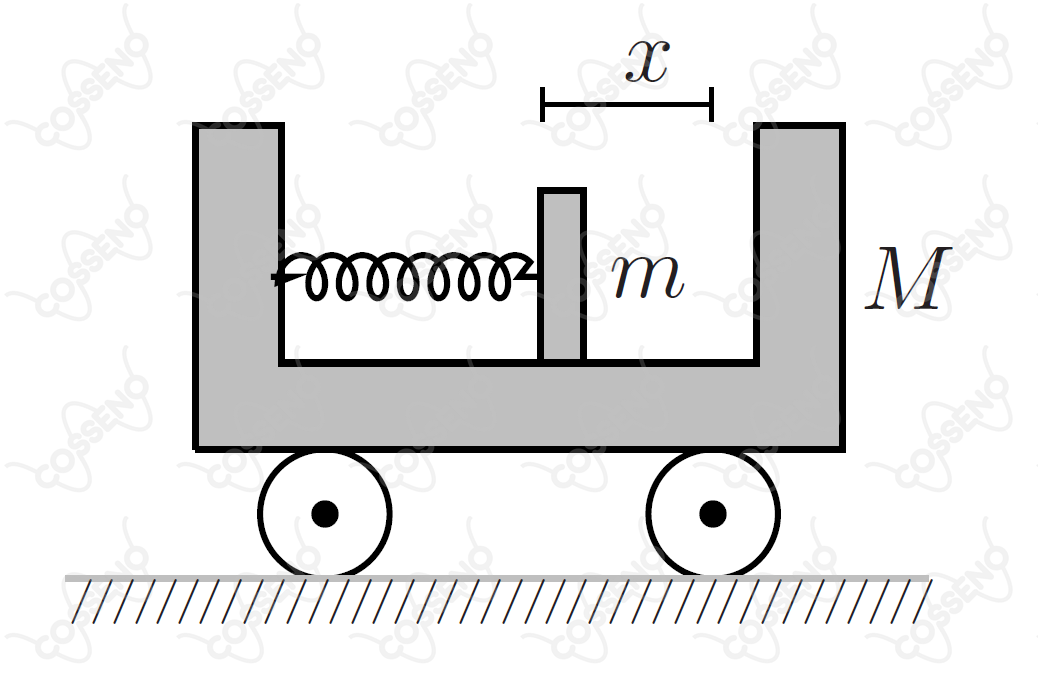
Sendo o sistema então abandonado e considerando que não há atrito, pode-se afirmar que o valor inicial da aceleração do bloco relativa ao carrinho é
$\color{Highlight}{\textit{Considerar o referencial do solo para efeitos de}}$ $\color{Highlight}{\textit{c}}$$\color{Highlight}{\acute{a}}$$\color{Highlight}{\textit{lculo.}}$
Aplicando a 2º Lei de Newton para o carrinho:
$$
kx = Ma
$$
$$
a =\frac{kx}{M} \tag{1}
$$
Aplicando a 2º Lei de Newton para o bloco:
$$
kx = m ( \gamma - a)
$$
Isolando $\gamma $
$$
\gamma = \frac{kx}{m} + a \tag{2}
$$
$(1)$ em $ (2)$:
$$
\gamma = \frac{kx}{m} + \frac{kx}{M} = \frac{kx}{m M} (m+M)
$$
Alternativa correta: $ \boxed{\mathrm{E}} $
$$
\boxed{\gamma = \frac{kx(m+M)}{m M} }
$$
