Uma partícula de massa está sujeita exclusivamente à ação da força , que varia de acordo com o gráfico da figura, sendo o versor no sentido positivo de .
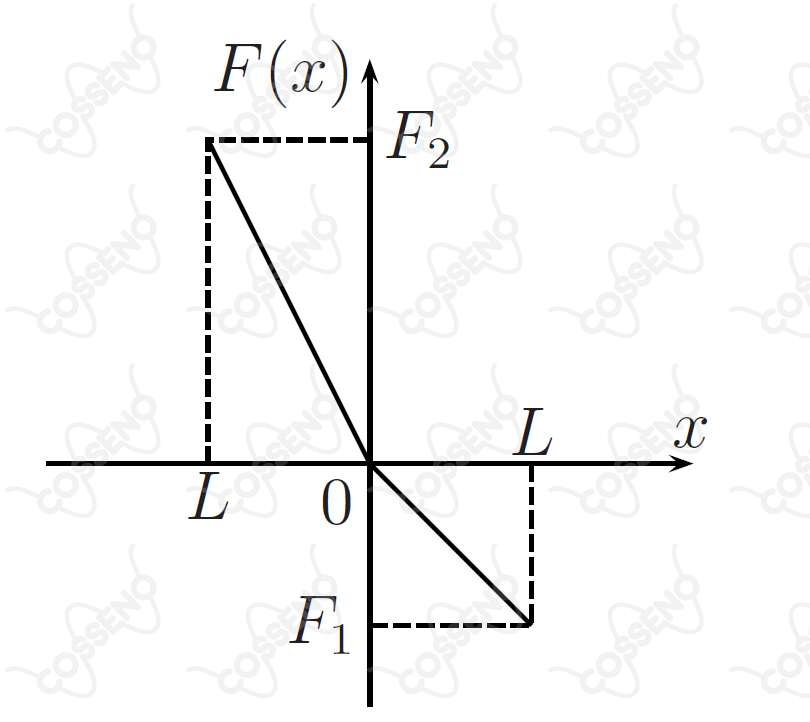
Se em , a partícula se encontra em com velocidade no sentido positivo de , pedem-se:
a) O período do movimento da partícula em função de e .
b) A máxima distância da partícula à origem em função de e .
c) Explicar se o movimento descrito pela partícula é do tipo harmônico simples.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$(a)$ Sabe-se que a equação do período é dada por
$$T = 2\pi \sqrt{\dfrac{m}{k}}.$$
Vendo a equação acima, nossa missão é encontrar a constante $k$ do sistema. Perceba uma coisa, a força $F_{2}$ no gráfico é desenhada em módulo, maior que a força $F_{1}$, o que nos dá uma ideia de que seja diferente as constantes, pois mesmo com forças diferentes, o deslocamento ainda é o mesmo em módulo. Vejamos as equações para o equilíbrio em cada situação.
$$F_{1} = k_{1}L \ , \ F_{2} = k_{2}L \\ k_{1} = \dfrac{F_{1}}{L} \ , \ k_{2} = \dfrac{F_{2}}{L}.$$
Perceba uma coisa, as forças e as constantes são diretamente proporcionais, logo se a força $F_{2}$ é maior, a constante $k_{2}$ deve também ser maior e isso faz muito sentido, pois se a constante não mudasse ou fosse menor, o deslocamento não seria $L$, seria $L + x$, em que $x$ é um deslocamento adicional. Pense na constante como se fosse uma resistência que está querendo impedir movimento, isto é, querendo manter o estado natural, a natureza sempre tenta manter o estado natural e essa força está querendo provocar um pertubação não natural. Com isso, veja que
$$T = \dfrac{T}{2} + \dfrac{T}{2} = \dfrac{2\pi}{2}\left(\sqrt{\dfrac{mL}{F_{1}}} + \sqrt{\dfrac{mL}{F_{2}}}\right) \Rightarrow$$
$$\Rightarrow \boxed{(a) \ T = \pi \left(\sqrt{\dfrac{mL}{F_{1}}} + \sqrt{\dfrac{mL}{F_{2}}}\right)}$$
$(b)$ A máxima distância da partícula em relação à origem é atingida quando toda a energia cinética do sistema é convertida em energia potencial. Portanto, é possível escrever que
$$\dfrac{mv^{2}}{2} = \dfrac{kx^{2}}{2}.$$
Na equação de conservação acima, temos que toda a energia cinética sendo igualada a uma energia potencial, isto é, uma conservação no ponto inicial ($K_{máx}$) e outra no ponto máximo ($U_{máx}$). Você pode enxergar isso a partir da própria equação de movimento do $MHS$, lembre-se que
$$x = A\cos (\omega t) \ , \ v = - \omega A \sin \omega t.$$
Se o seno for zero, o cosseno será igual a 1 pelo teorema fundamental da trigonometria caracterizando a distância máxima e toda sua energia cinética convertida em potencial. Daí,
$$\dfrac{mv^{2}}{2} = \dfrac{F_{1}x_{1}^{2}}{2L} \ \text{ou} \ \dfrac{mv^{2}}{2} = \dfrac{F_{2}x^{2}_{2}}{2L} \Rightarrow$$
$$\Rightarrow x_{1} = v^{2}\sqrt{\dfrac{mL}{F_{1}}} \ \text{ou} \ x_{2} = v^{2}\sqrt{\dfrac{mL}{F_{2}}}.$$
Qual dessas duas velocidades é máxima? Lembre-se que $F_{2} > F_{1}$, então $x_{1}$ é a máxima distância da partícula.
$$\boxed{(b) \ x_{1} = v^{2}\sqrt{\dfrac{mL}{F_{1}}}}.$$
$(c)$ Apesar de parecer muito, não se trata de um MHS, pois veja que os períodos são diferentes e isso é o primeiro caso para se classificar um MHS, além disso, as amplitudes são diferentes.

