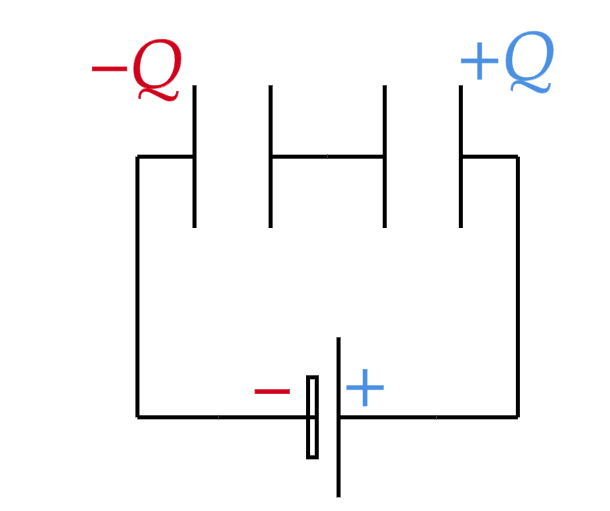
Dois capacitores em série , de capacitância e , respectivamente, estão sujeitos a uma diferença de potencial . O Capacitor de capacitância tem carga e está relacionado com através de , sendo um coeficiente de proporcionalidade. Os capacitores carregados são então desligados da fonte e entre si, sendo a seguie religados com os respectivos terminais de carga de mesmo sinal. Determine o valor de para que a carga final do capacitor de capacitância seja .
CossenoGPT
Teste
gratuitamente agora
mesmo! 

No início, têm-se dois capacitores em série, assim como conhecemos a carga de uma deles, esta que é igual a $Q_1$. Ou seja, nós sabemos a carga do segundo capacitor, pois se ambos estão em série, a indução total nos garante que a carga em $C_2$ será igual a em $C_1$.
 Noutro momento, após o carregamento, ligam-se os capacitores entre si, num arranjo como abaixo:
Noutro momento, após o carregamento, ligam-se os capacitores entre si, num arranjo como abaixo:
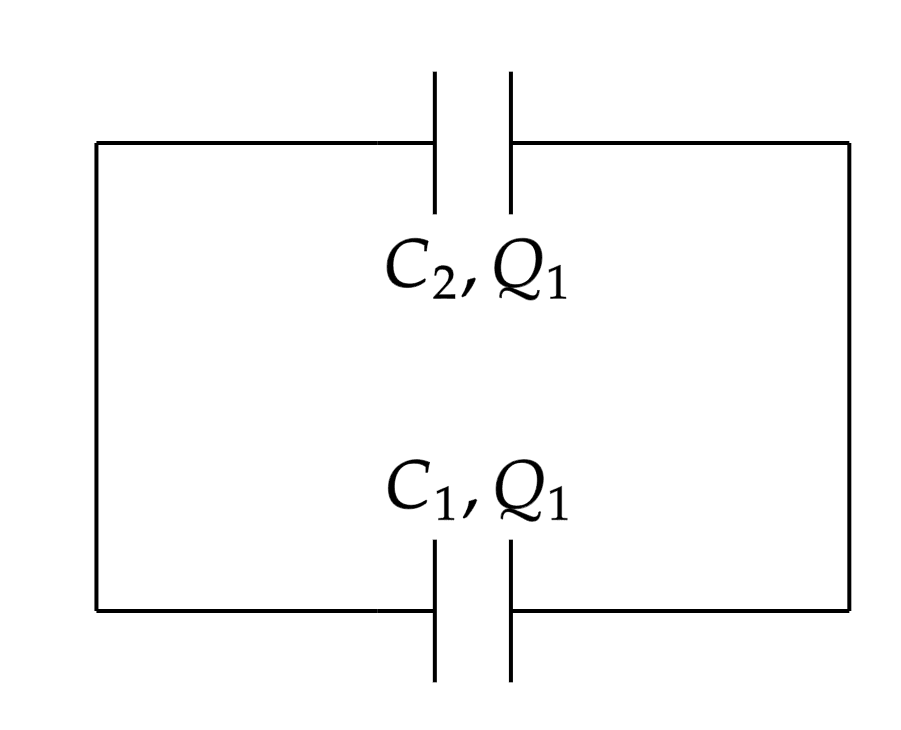 Pela conservação da carga: \begin{matrix}
\sum Q_{inicial} =\sum Q_{final}
\end{matrix}Então, após certo tempo:\begin{matrix}
Q_1 + Q_1 = \dfrac{Q_1}{4} + Q^{*}_1 &\therefore& Q^{*}_1 = \dfrac{7Q_1}{4}
\end{matrix}Já que os capacitores estão expostos a mesma diferença de potencial, segue: \begin{matrix}
\dfrac{(Q_1/4)}{C_2} = \dfrac{(Q^{*}_1)}{C_1} &\Rightarrow& x = \dfrac{(Q_1/4)}{Q^{*}_1} &\therefore& x = \dfrac{1}{7} \ \ \tiny{\blacksquare}
\end{matrix}
Pela conservação da carga: \begin{matrix}
\sum Q_{inicial} =\sum Q_{final}
\end{matrix}Então, após certo tempo:\begin{matrix}
Q_1 + Q_1 = \dfrac{Q_1}{4} + Q^{*}_1 &\therefore& Q^{*}_1 = \dfrac{7Q_1}{4}
\end{matrix}Já que os capacitores estão expostos a mesma diferença de potencial, segue: \begin{matrix}
\dfrac{(Q_1/4)}{C_2} = \dfrac{(Q^{*}_1)}{C_1} &\Rightarrow& x = \dfrac{(Q_1/4)}{Q^{*}_1} &\therefore& x = \dfrac{1}{7} \ \ \tiny{\blacksquare}
\end{matrix}

Ampliar Imagem

Ampliar Imagem

