Denotemos $w =-2iz$ e $z = (a,b)$, então:\begin{matrix} z = (a,b )&\wedge& w = (2b,-2a) \end{matrix}$\color{orangered}{\text{Obs:}}$ Caso tenha dificuldade com o passo acima, pense na forma algébrica, exemplo:\begin{matrix} z = a+ bi &\Rightarrow& -2iz =-2ai -2bi^2 &\therefore& w = 2b - 2ai \end{matrix}Sabido que o argumento de um complexo é o ângulo formado entre o eixo real e o módulo do complexo, tomemos $\text{arg}(w) = \theta$, tal que no plano de Argand-Gauss:\begin{matrix} z: & \tan(\pi/4) = \dfrac{b}{a} &\wedge& w: & \tan(\theta) = \dfrac{-2a}{\phantom{-}2b} \end{matrix}Consequentemente,\begin{matrix} \tan(\theta) = -\cot{(\pi/4)} \end{matrix}$• \ \text{Caminho I:}$ Agora, pode-se partir para manipulações trigonométricas como abaixo:\begin{matrix} -\cot{(\pi/4)} =-\tan{(\pi/4)} = \tan(2\pi - \pi/4)^* \end{matrix}\begin{matrix}\boxed{\tan(\theta) = \tan{(7\pi/4)} } \end{matrix}$\color{#3868b8}{\text{Adendo:}}$ Observe que a passagem $(*)$ é vinculada ao fato do eixo imaginário ser negativo, ou seja, não é válido escrever $ \tan(\pi - \pi/4)$, pois isso varreria o argumento do simétrico ($2iz$). Caso essa passagem tenha ficado abstrata demais, veja outra opção a seguir. $• \ \text{Caminho II:}$ Visto que $\tan(\theta) = -\tan{(\pi/4)} = \tan{(-\pi/4)}$, pode-se esboçar no plano de Argand-Gauss: 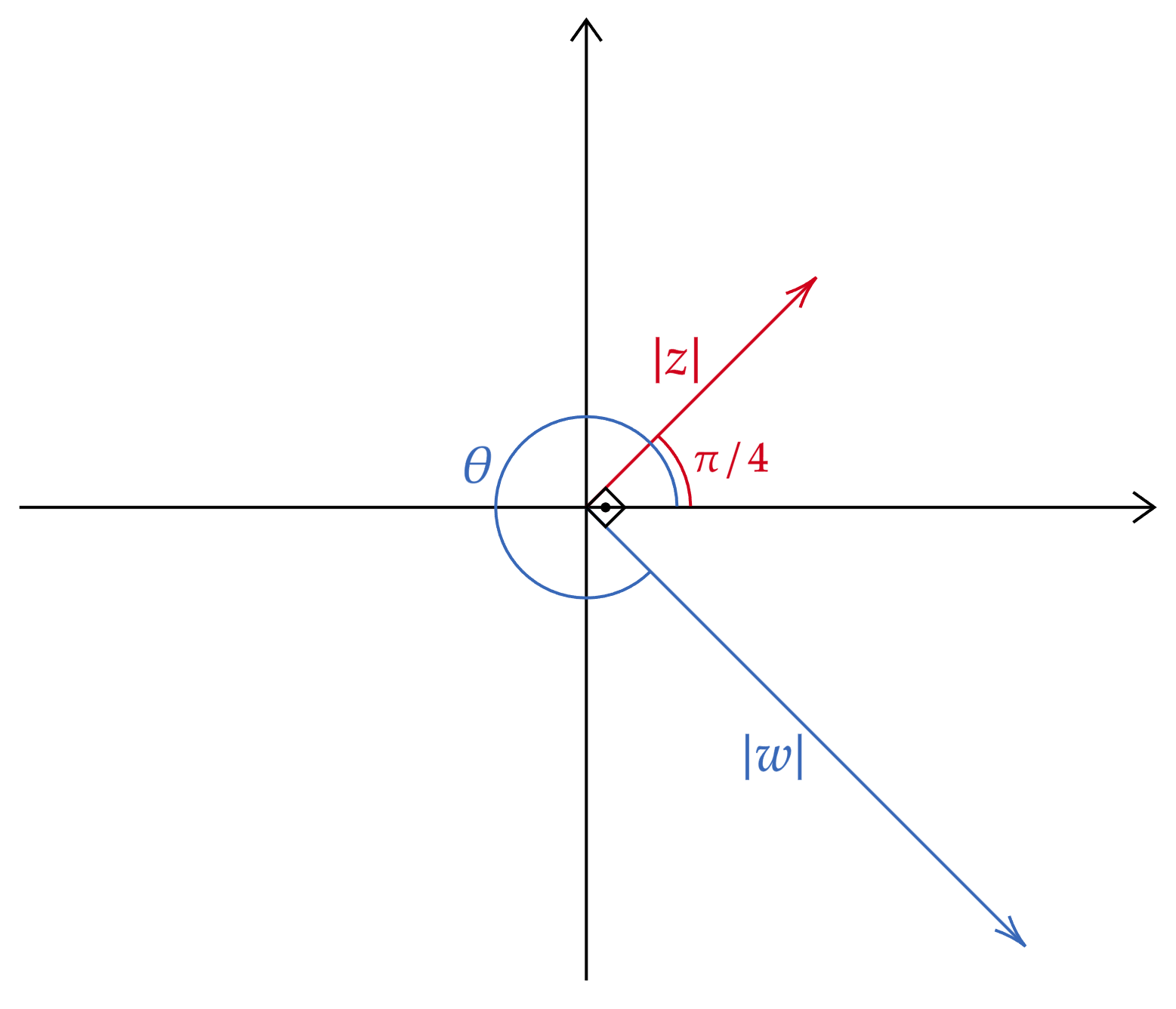Como resultado, \begin{matrix} \theta = 2\pi - \dfrac{\pi}{4} &\therefore& \text{arg}(-2iz) = \dfrac{7\pi}{4} \ \ \tiny{\blacksquare} \end{matrix}\begin{matrix}Letra \ (E) \end{matrix}

Do enunciado, temos que $z = \large{\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i}$ , logo: $-2\cdot iz = \large{-2\cdot(-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i})$ $=$ $\large{2\cdot(\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i)}$ $=$ $\large{2\cdot cis(\frac{7\pi}{4})}$ Assim, $-2iz$ tem argumento $\boxed{\large{\frac{7\pi}{4}}}$ Conclusão: perceba que é fácil encontrar o argumento, quando interpreta-se os sinais dos valores do seno e do cosseno na forma trigonométrica de $-2iz$, no caso, o cosseno é positivo e o seno é negativo, e isto só é possível no quarto quadrante. Além disso, o seno e cosseno, em módulo, possuem o mesmo valor, e isto só é possível quando, no quarto quadrante, se faz um ângulo $\Large{2\pi - \frac{\pi}{4} = \frac{7\pi}{4}}$.