Um problema clássico da cinemática considera objetos que, a partir de certo instante, se movem conjuntamente com velocidade de módulo constante a partir dos vértices de um polígono regular, cada qual apontando à posição instantânea do objeto vizinho em movimento. A figura mostra a configuração desse movimento múltiplo no caso de um hexágono regular.
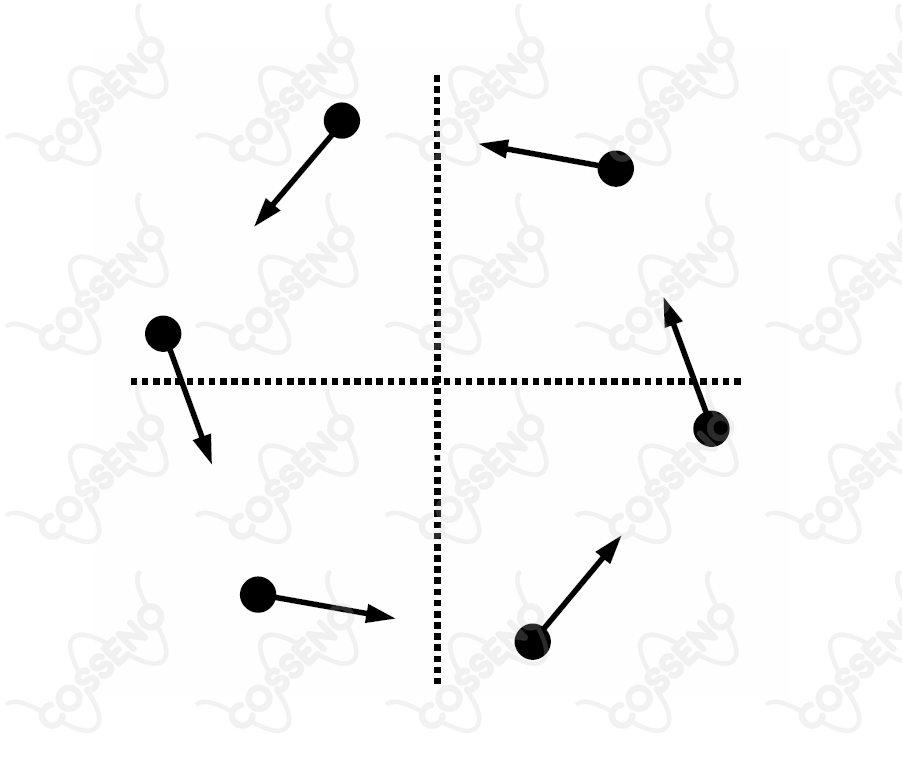
Considere que o hexágono tinha de lado no instante inicial e que os objetos se movimentam com velocidade de módulo constante de . Após quanto tempo estes se encontrarão e qual deverá ser a distância percorrida por cada um dos seis objetos?
CossenoGPT
Teste
gratuitamente agora
mesmo! 

este problema pode ser resolvido de uma forma mais trivial decompondo a velocidade centripeta $Vctp=V\cos \frac{\pi } {3}$
logo como $t=\frac{d}{v}$ T=10s e D=20m, a outra solução se torna inviável no tempo de prova, mas a ideia pode ser util na resolução de outros problemas

23:06 03/09/2021
Boa! Questão clássica, legar para o pessoal começar a "pensar fora da caixa" em cinemática.
Este problema pode ser resolvido com velocidade relativa de modo que considerando duas particulas A e B:
$ Va=Vax\cdot \hat{i} + Vay \cdot \hat{j} $
$ Vb=Vbx \cdot \hat{i} + Vby \cdot \hat{j} $
de modo que a velocidade relativas entre elas é V:
$ V=Va-Vb=(Vax-Vbx) \cdot \hat{i} +(Vay-Vby) \cdot \hat{j} $
logo:
$ -dr=Vx\cdot dt $ e
$ r\cdot d\Theta =Vy\cdot dt $ (cinematica angular)
dividindo as equações $ \frac{-dr}{r}=\frac{Vx}{Vy}\cdot d \Theta $
portanto:
$ r=ro\cdot e^{-{\int \frac{Vx}{Vy}d\Theta} } $ a partir desta equação podemos achar o tempo de encontro de modo que $r\cdot d\Theta =Vy\cdot dt $ logo:
$ t=ro\cdot \int \frac{e^{-{\int \frac{Vx}{Vy}d\Theta} }}{Vy}d\Theta $
aplicando estas formulas de velocidade relativa no hexagono chegamos que: $ V=V/2 \cdot \hat{i}-V\cdot \frac{3^{1/2}}{2} $
de modo que $Vy=\frac{V}{2}$ no calculo do t chegamos em $ t=2\cdot \frac{l}{t} $ logo T=10s, no calculo da distancia é só aplicar $ d=v\cdot t $ D=20m


