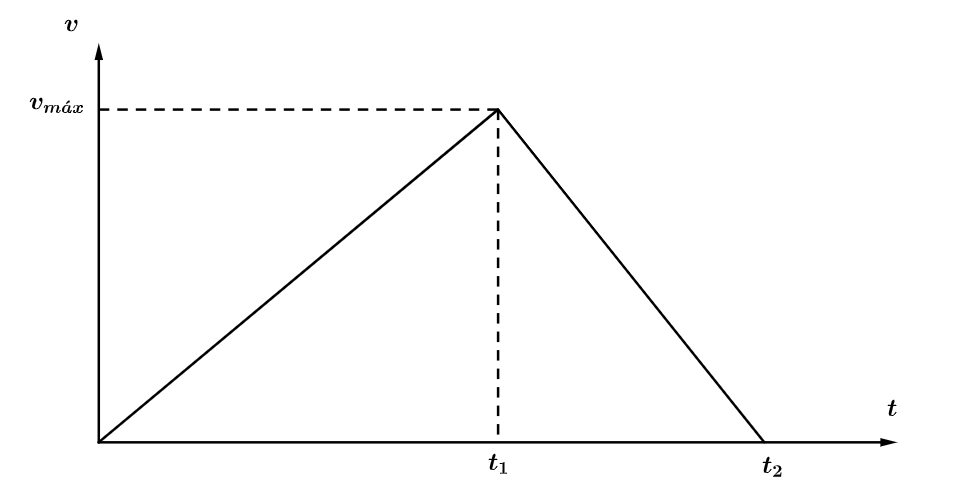
O problema deve ser dividido em duas etapas: $\text{Etapa 1:}$ O corpo sobe com tempo mínimo, isto é, com aceleração $a_{1}$ máxima. Sabendo disso, pode-se aplicar a segunda lei de Newton para o bloco, obtendo $$a_{1} = (n-1)g.$$ $\text{Etapa 2:}$ O corpo deve voltar para repouso com maior aceleração possível, isso acontece quando a tração é nula. Portanto $$v_{máx} = a_{1}t_{1} = g(t_{2} - t_{1}) \Rightarrow \\ \Rightarrow (n-1)gt_{1} = g(t_{2} - t_{1}) \Rightarrow \\ \Rightarrow t_{2} = nt_{1}.$$ $$v_{máx} = g\left(t_{2} + \dfrac{t_{2}}{n}\right).$$ Pode-se calcular $H$ a partir da área do gráfico acima. Com isso, $$t_{2} = \sqrt{\dfrac{2nH}{(n--1)g}}.$$