A princípio, podemos começar esboçando a situação: 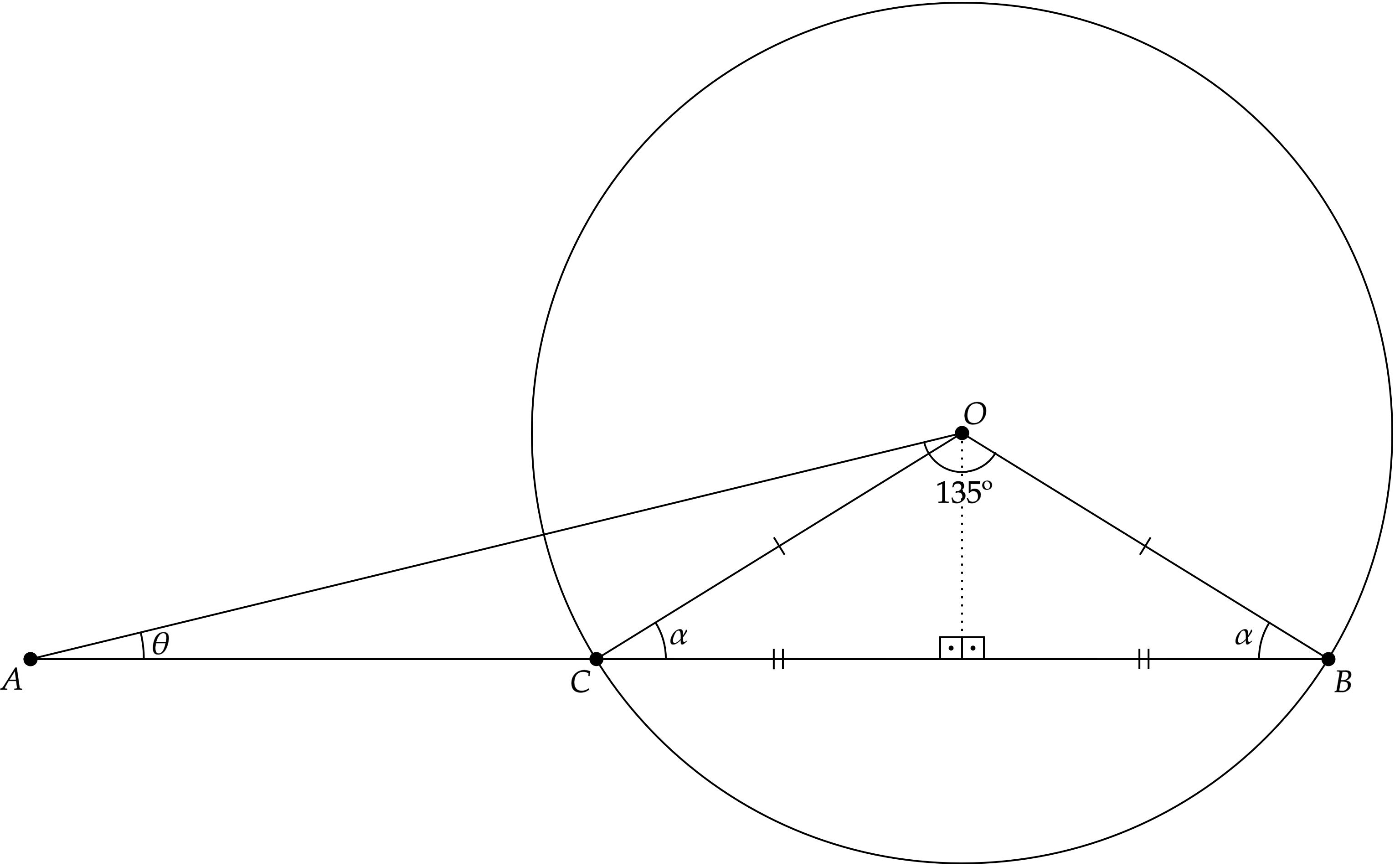$• \ \text{a)}$ Conhecida a lei dos senos, pode-se escrever:\begin{matrix} \dfrac{\overline{OB}}{\sin{\theta}} = \dfrac{\overline{AB}}{\sin{135º}} &\therefore&\sin{\theta} = \sqrt{\dfrac{1}{2} - \dfrac{\sqrt{3}}{4}} \end{matrix}Pondere que,\begin{matrix} \sqrt{\dfrac{1}{2} - \dfrac{\sqrt{3}}{4}} = \sqrt{\dfrac{1}{2} \left(1 - \dfrac{\sqrt{3}}{2}\right)} = \sqrt{\dfrac{1}{2} \left(1 - \cos{30º}\right)} \end{matrix}Conhecido o cosseno da soma, mais precisamente o arco duplo, têm-se:\begin{matrix} \cos{30º} = 1 - 2 \sin^2{15º} \end{matrix}Consequentemente,\begin{matrix}\sin{\theta} = \pm \sin{15º} \end{matrix}Observe que a raiz negativa é inviável pois estamos falando de um triângulo, portanto:\begin{matrix} \theta = 15º \ \ \tiny{\blacksquare} \end{matrix}$• \ \text{b)}$ Conforme resultado anterior, facilmente verificamos que $\alpha = 30º$, visto que para o triângulo $AOB$:\begin{matrix} \theta + 135º + \alpha = 180º \end{matrix}Por outro lado, analisando o triângulo $AOC$, verificamos que ele também é isósceles, afinal, o suplemento de $\alpha$ é $A\hat{C}O = 150º$, em que:\begin{matrix} A\hat{C}O + \theta + A\hat{O}C = 180º &\therefore& A\hat{O}C = \theta = 15º \end{matrix}Como o triângulo é isósceles, têm-se:\begin{matrix} \overline{AC} = \overline{CO} = \sqrt{2 - \sqrt{3}} \ \ \tiny{\blacksquare} \end{matrix}