Em tese, a questão se resume em conseguir construir ou ao menos interpretar a situação do enunciado. No caso, a partir do que foi exposto, pode-se esboçar: 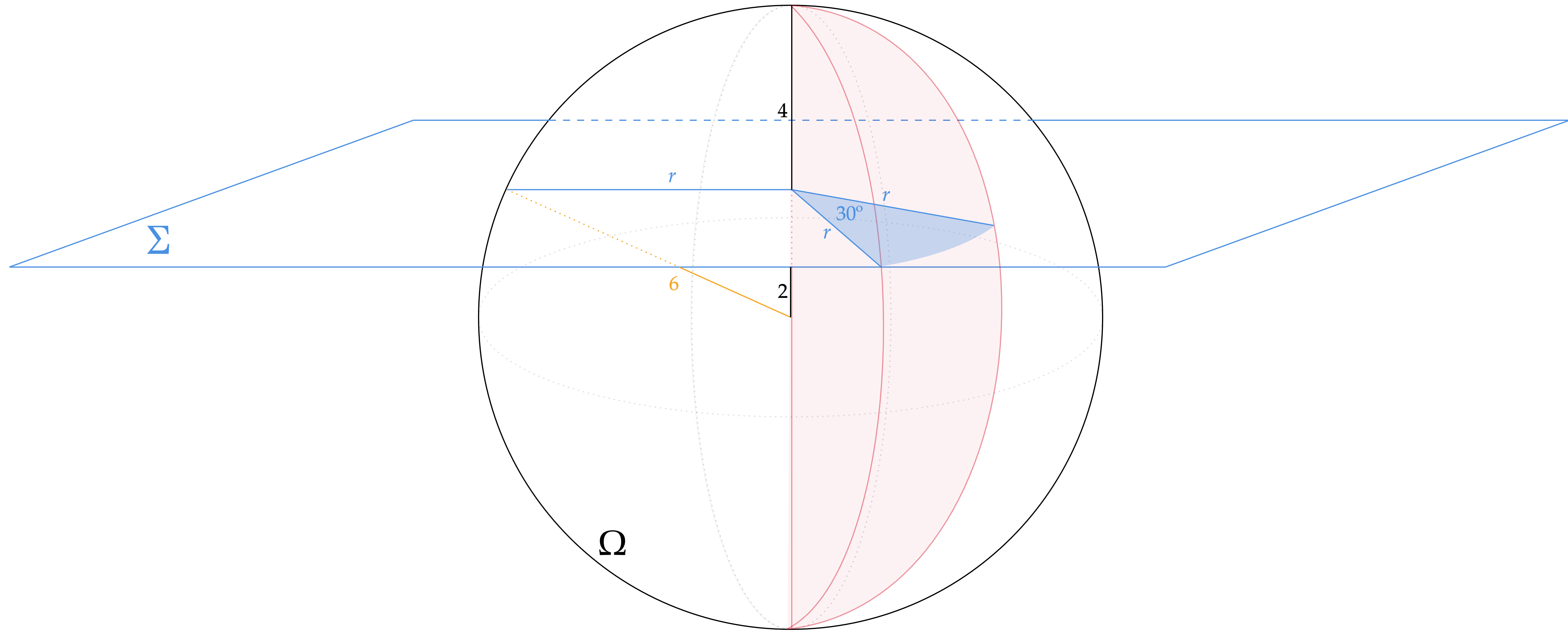Observe que a área que precisamos calcular é simplesmente a área $S$ de um setor circular de $30º$ e raio $r$. Para isso, necessitamos apenas de $r$, o que pode ser encontrado pelo teorema de Pitágoras, conforme imagem:\begin{matrix} 6^2 = 2^2 + r^2 &\therefore& r = 4\sqrt{2} \ \pu{cm} \end{matrix}Portanto, para a área do setor, esta que é a mesma da intersecção do plano $\sum$ com a cunha esférica, têm-se:\begin{matrix} S = \left(\dfrac{30º}{360º}\right) (\pi r^2) &\therefore& S = \dfrac{8\pi}{3} \ \pu{cm^2} \ \ \tiny{\blacksquare} \end{matrix}