Conhecendo os sólidos em questão, assim como a inscrição dos mesmos, pode-se esboçar a situação abaixo: 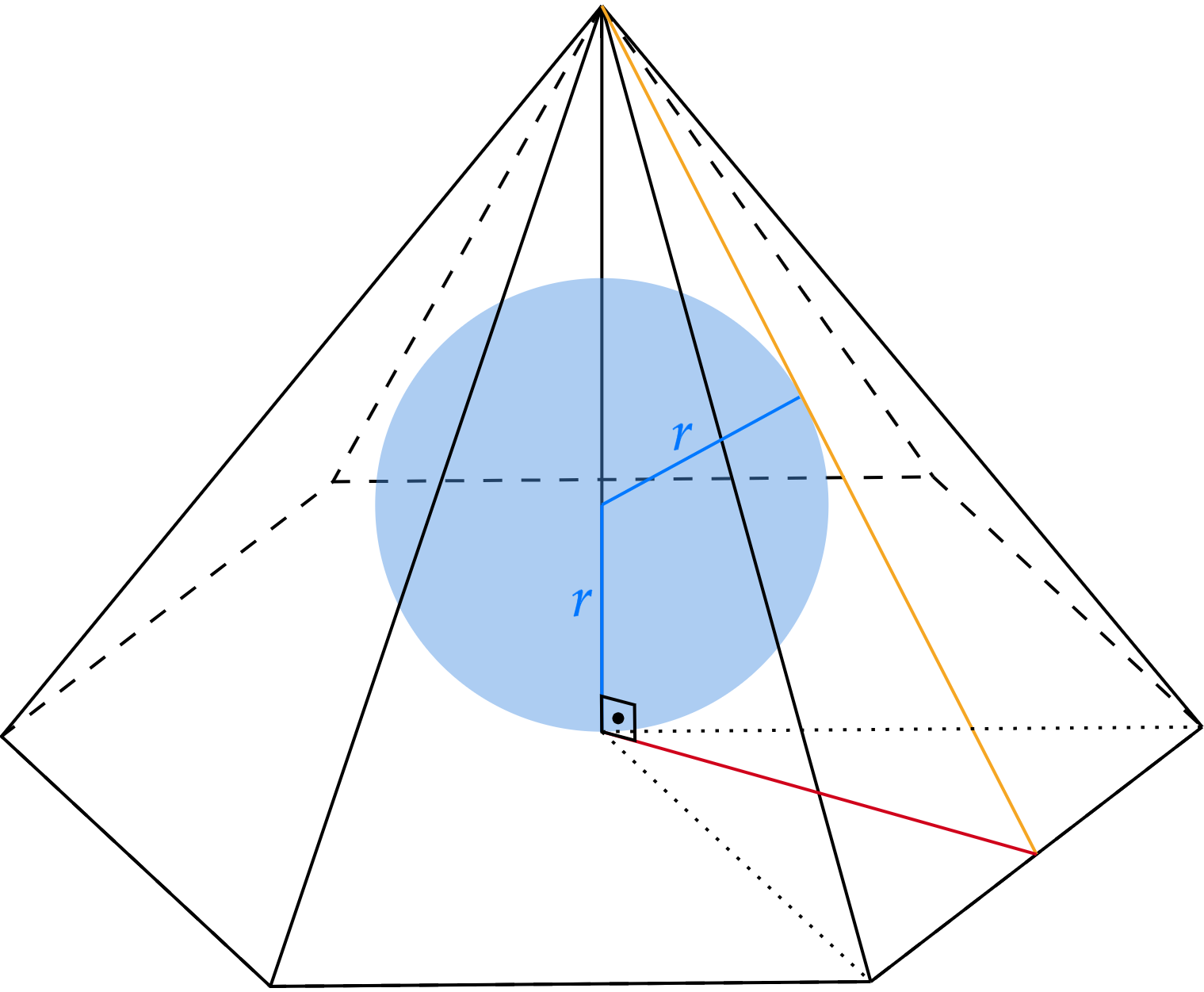Como sabemos a aresta da base e a altura da pirâmide, podemos trabalhar o problema planificando a situação: 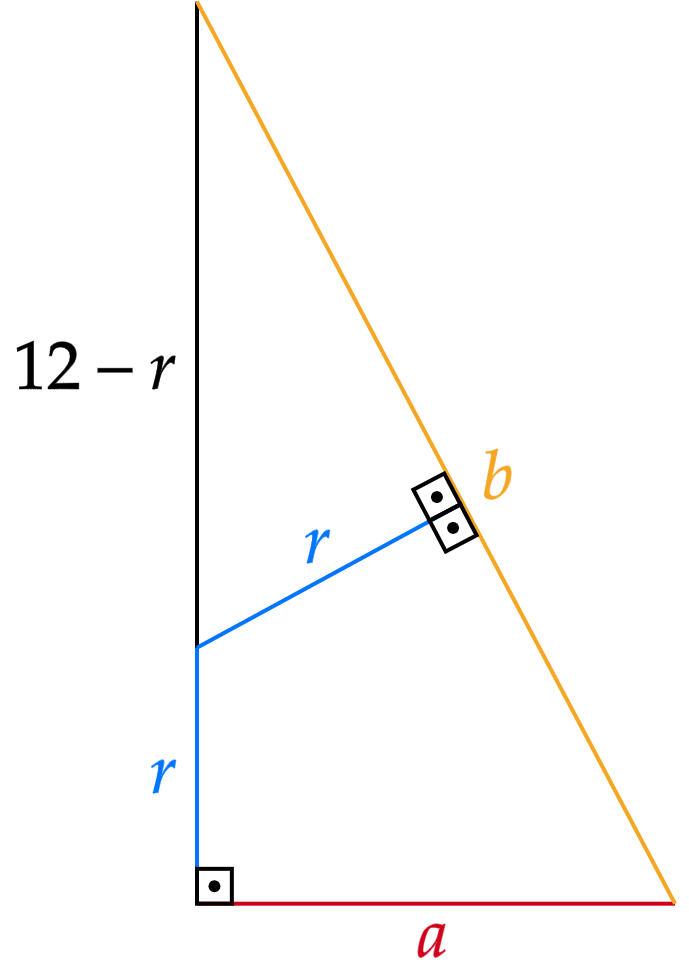Observe que $a$ é a altura de um dos $6$ triângulos equiláteros que compõem a base, ou seja:\begin{matrix} a = \dfrac{\dfrac{10\sqrt{3}}{3} \cdot \sqrt{3}}{2} = 5 \ \pu{cm} \end{matrix}Consequentemente, aplicando o teorema de Pitágoras:\begin{matrix} b^2 = a^2 + 12^2 &\therefore& b = 13 \ \pu{cm} \end{matrix}Por fim, resta-nos apenas fazer uma semelhança de triângulos, tal que:\begin{matrix} \dfrac{r}{12-r} = \dfrac{5}{12} &\therefore& r = \dfrac{10}{3} \ \pu{cm} \end{matrix}\begin{matrix}Letra \ (E) \end{matrix}