A princípio, sabemos que o triângulo é obtusângulo em $A\hat{B}C$, ou seja, a altura relativa ao lado $\overline{AB}$ é externa ao triângulo, tal que podemos esboçar a situação como: 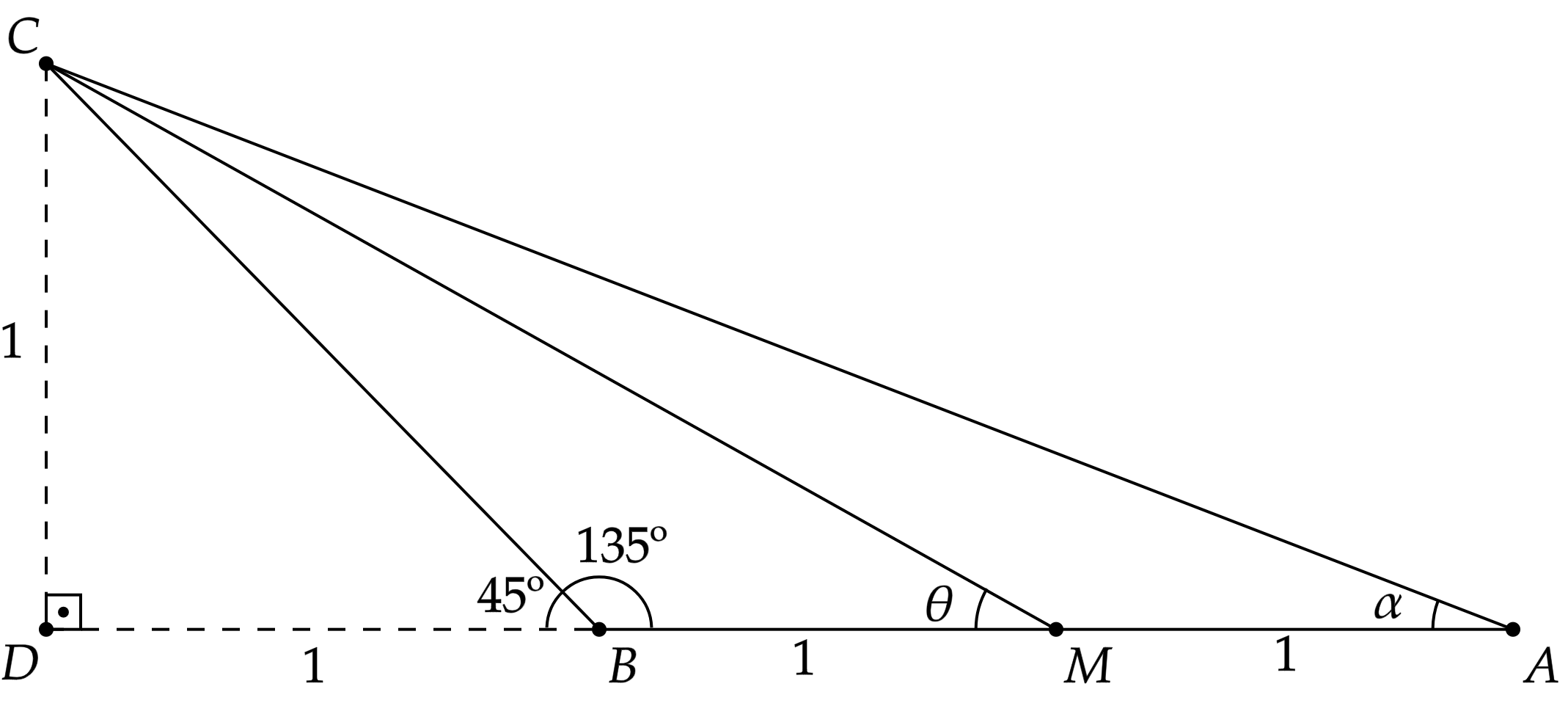Com isso, pensando em relacionar os ângulos $\alpha$ e $\theta$, que são, respectivamente, $A\hat{B}C$ e $B\hat{M}C$, têm-se:\begin{matrix} \tan{(\alpha + \theta)} = \dfrac{\tan{\alpha}+\tan{\theta}}{1 - \tan{\alpha}\tan{\theta}} = \dfrac{\dfrac{1}{3}+ \dfrac{1}{2}}{1 - \dfrac{1}{3} \cdot \dfrac{1}{2}} = 1 \end{matrix}Como $0 < (\alpha + \theta) < \pi$, concluímos que:\begin{matrix} (\alpha + \theta) = \dfrac{\pi}{4} \end{matrix}\begin{matrix}Letra \ (B) \end{matrix}

Outra solução: A figura proposta pelo problema inicialmente pode ser visto como um retângulo. Sabendo disso, tome a iniciativa de duplicar o retângulo para cima e formar o $\triangle AHC$. 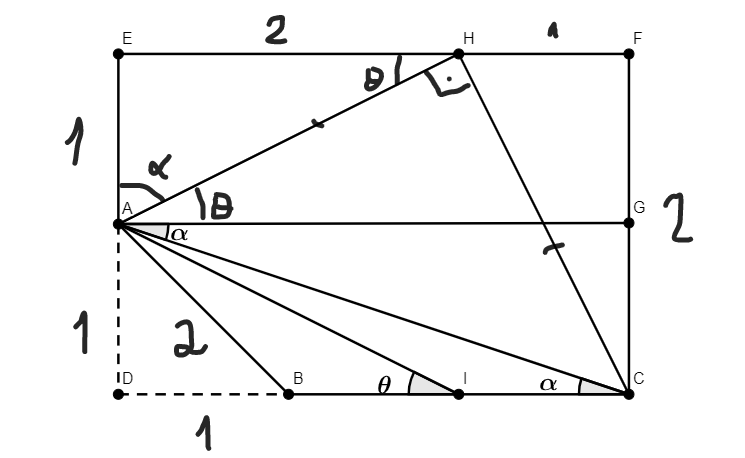Veja que na figura os $\triangle AEH$ e $\triangle HFC$ são congruentes. Os ângulos $G\hat{A}C$ e $H\hat{A}G$ aparecem devido ao paralelismo (alterno interno). Com isso, veja que o triângulo $\triangle AHC$ é retângulo e isósceles, logo $\alpha + \beta = 45^\circ.$