Determine todos os valores de tais que a equação tenha duas raízes reais distintas e maiores que zero.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A princípio, podemos pensar nas raízes distintas, para isso, basta o discriminante $(\Delta)$ da equação de segundo grau ser maior que zero, ou seja:\begin{matrix}
\Delta = (2m)^2 - 4(2-m)(m+2) > 0 \\ \\ m^2 > 0
\end{matrix}Consequentemente,\begin{matrix}
\text{(I)}: & {m > \sqrt{2} \ \ \vee \ \ m < - \sqrt{2} }
\end{matrix}Por outro lado, as raízes devem ser maiores do que zero, assim, conhecida as $\text{fórmulas de Viète}$, ou simplesmente a $\text{soma e produto}$ de raízes, têm-se:\begin{matrix}
x_1 + x_2 = \dfrac{2m}{m-2} > 0 &,& x_1 \cdot x_2 = \dfrac{m+2}{2-m}> 0
\end{matrix}A partir da soma, constata-se:\begin{matrix}
\text{(II)}: & {m > {2} \ \ \vee \ \ m < 0 }
\end{matrix}Já o produto:\begin{matrix}
\text{(III)}: & {m > {-2} \ \ \vee \ \ m < 2 }
\end{matrix}Por fim, resta-nos fazer o último estudo do sinal, este que engloba todos os resultados encontrados, o que pode ser feito como:
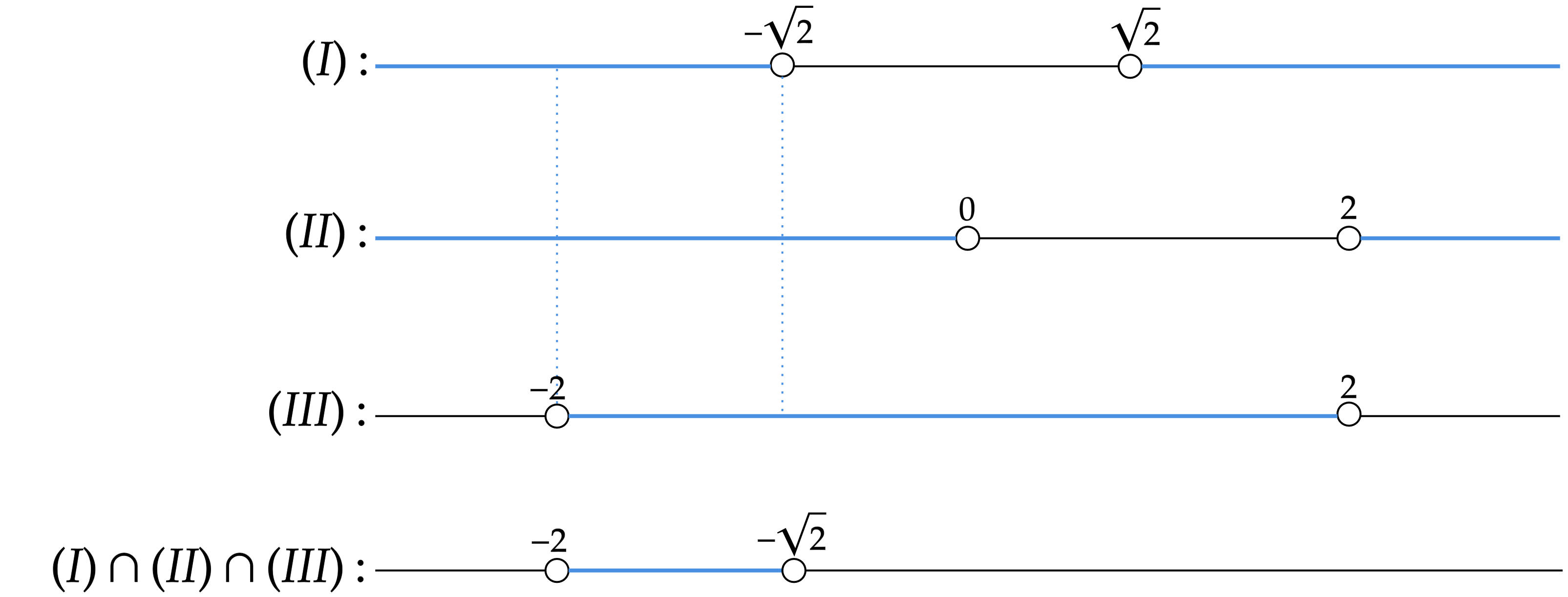 Portanto,\begin{matrix}m \in \ ] -2, -\sqrt{2} \ [ & \tiny{\blacksquare}
\end{matrix}
Portanto,\begin{matrix}m \in \ ] -2, -\sqrt{2} \ [ & \tiny{\blacksquare}
\end{matrix}

Ampliar Imagem

