A princípio, como $\overline{AB}$ é o diâmetro, sabemos que o triângulo $ABC$ será retângulo - você pode verificar isso pensando no arco-capaz. Nesse sentido, esboçando a situação descrita, temos: 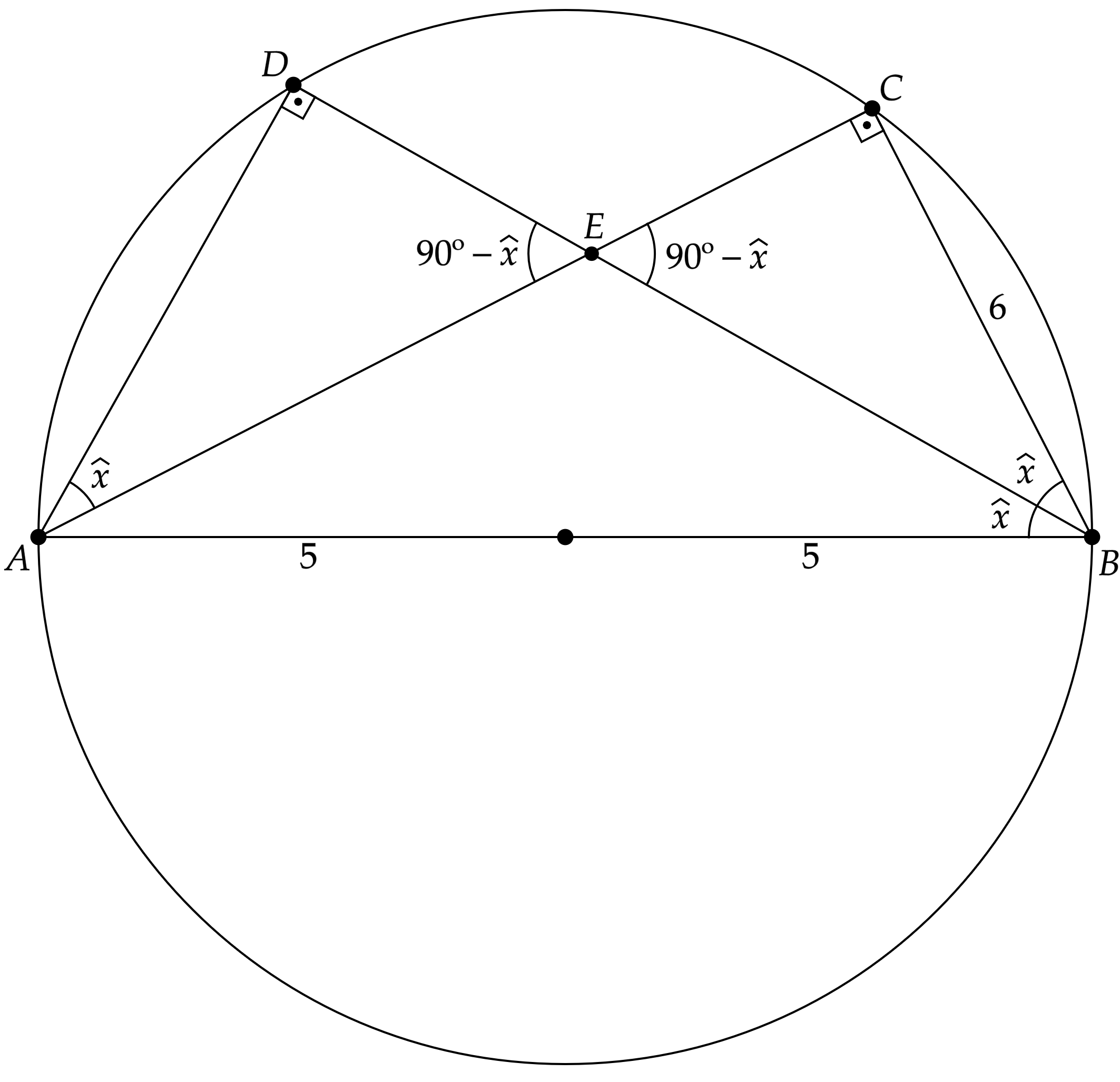Comecemos por observar que: \begin{matrix} \alpha = [ABC] + [ABD] &,& \beta = [ABC] - [BCE] = [ABD] - [ADE] \end{matrix}Consequentemente, \begin{matrix}\alpha - 2\beta = [BCE] + [ADE] \end{matrix}Veja que podemos começar utilizando o $\text{teorema da Bissetriz interna}$:\begin{matrix}\dfrac{\overline{AE}}{10} = \dfrac{\overline{CE}}{6} &,& \overline{AE} + \overline{CE} = \overline{AC} \end{matrix}Consequentemente, constatamos:\begin{matrix} \overline{AE} = 5 \ \pu{cm} &,& \overline{CE} = 3 \ \pu{cm} \end{matrix}Agora, já podemos encontrar a área do triângulo $BCE$, ela é:\begin{matrix} [BCE] = \dfrac{\overline{BC} \cdot \overline{CE} }{2} &\therefore& [BCE] = 9 \ \pu{cm^2} \end{matrix}Por outro lado, pensando na área de $ADE$, pode-se começar encontrando $\overline{BE}$ visando fazer uma semelhança de triângulos entre os triângulos $ADE$ e $BCE$. Com isso, pelo teorema de Pitágoras:\begin{matrix} \overline{BE}^2 = \overline{CE}^2 + \overline{BC}^2 &\therefore& \overline{BE} = 3\sqrt{5} \end{matrix}Continuando, por semelhança de triângulos:\begin{matrix} \dfrac{\overline{AD}}{\overline{AE}} = \dfrac{\overline{CE}}{\overline{BE}} &\therefore& \overline{AD} = 2\sqrt{5} \end{matrix}Novamente, por Pitágoras:\begin{matrix} \overline{AE}^2 = \overline{AD}^2 + \overline{DE}^2 &\therefore& \overline{DE} = \sqrt{5} \end{matrix}Dessa forma, a área do triângulo $ADE$ é:\begin{matrix} [ADE] = \dfrac{\overline{AD} \cdot \overline{DE} }{2} &\therefore& [ADE] = 5 \ \pu{cm^2} \end{matrix}Conclui-se então que:\begin{matrix} \alpha - 2\beta =14 \ \pu{cm^2}\end{matrix}\begin{matrix}Letra \ (A) \end{matrix}