A figura ao lado apresenta a curva de aquecimento de de uma substância pura genérica no estado sólido. Sabe-se que calor é fornecido a uma velocidade constante de . Admite-se que não há perda de calor para o meio ambiente, que a pressão é de durante toda a transformação e que a substância sólida apresenta apenas uma fase cristalina. Considere que sejam feitas as seguintes afirmações em relação aos estágios de aquecimento descritos na figura:
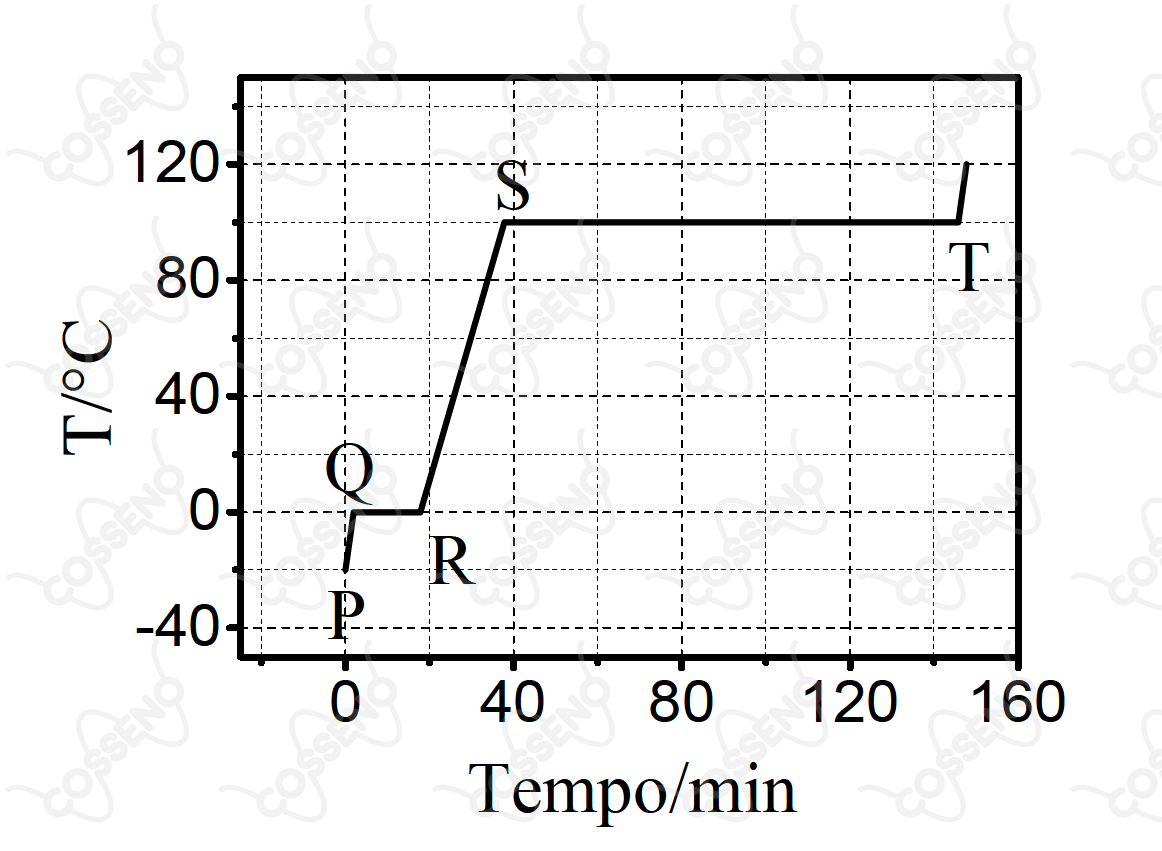
I. No segmento PQ ocorre aumento da energia cinética das moléculas.
II. No segmento QR ocorre aumento da energia potencial.
III. O segmento QR é menor que o segmento ST porque o calor de fusão da substância é menor que o seu calor de vaporização.
IV. O segmento RS tem inclinação menor que o segmento PQ porque o calor específico do sólido é maior que o calor específico do líquido.
Das afirmações acima, está(ão) ERRADA(S):
CossenoGPT


