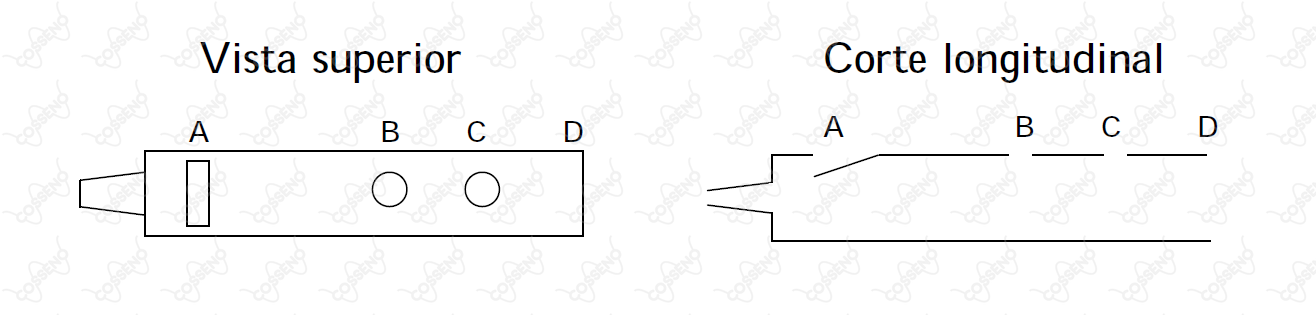
Considere o modelo de flauta simplificado mostrado na figura, aberta na sua extremidade , dispondo de uma abertura em (próxima à boca), um orifício em e outro em . Sendo , , e a velocidade do som de , as frequências esperadas nos casos:
(i) somente o orifício está fechado, e
(ii) os orifícios e estão fechados,
devem ser, respectivamente:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Com conhecimento acerca de tubos sonoros, mais precisamente dos abertos, o mais importante aqui é lembrar que em extremidades abertas sempre existe um ventre de deslocamento. No caso, estamos assumindo frequências fundamentais, o que nos permite esboçar a situação abaixo:
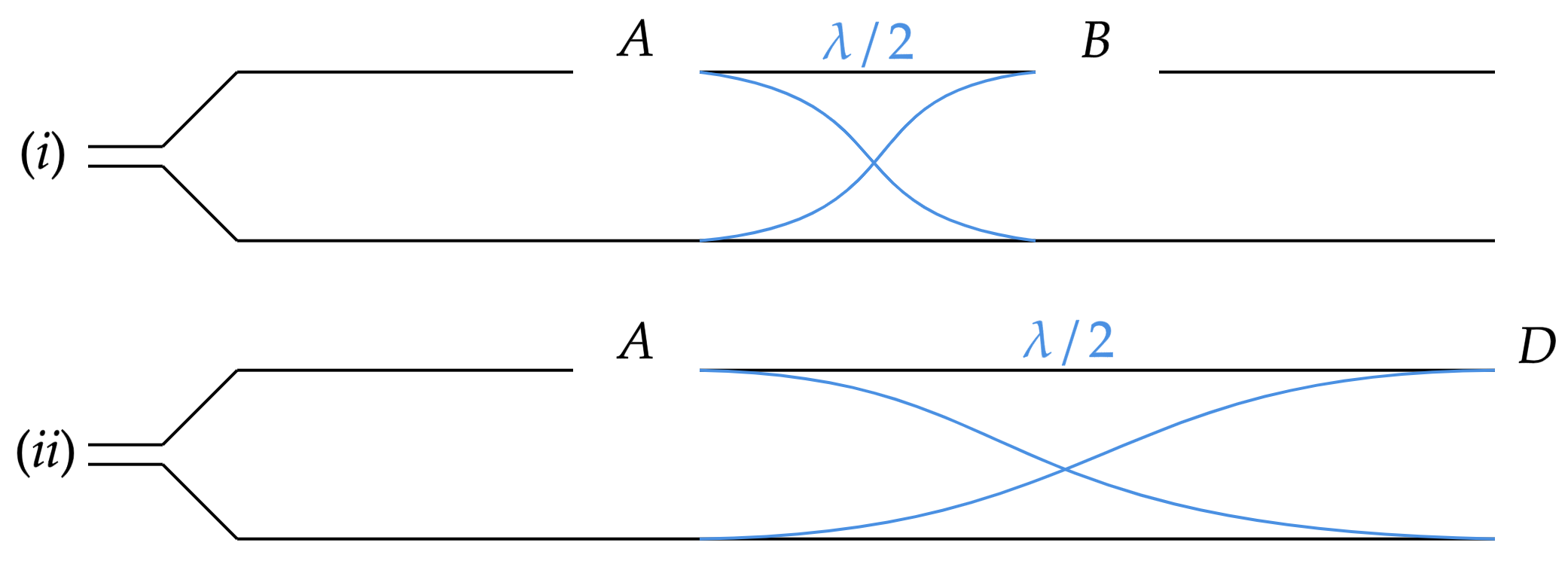 Observe que há uma diferença entre os comprimentos, e esta diferença será responsável pelos resultados distintos das frequências. Nesse sentido, encontrar $\overline{AB}$ não é difícil, visto que:\begin{matrix}
\overline{AB} +\overline{BD} = \overline{AD}
\end{matrix}Consequentemente,\begin{matrix}
2 \overline{AB} = 34 &\therefore& \overline{AB} = 17 \cdot 10^{-2} \ \pu{m}
\end{matrix}Pensando no comprimento de onda do caso $(i)$, têm-se:\begin{matrix}
\overline{AB} = \dfrac{\lambda_i}{2} &\therefore& \lambda_i =34 \cdot 10^{-2} \ \pu{m}
\end{matrix}Conforme equação fundamental da ondulatória:\begin{matrix}
v_{som} = \lambda_i f_{i} &\therefore& \boxed{ f_{i} = 1000 \ \pu{Hz}}
\end{matrix}Por outro lado, para o caso $(ii)$:\begin{matrix}
\overline{AD} = \dfrac{\lambda_{ii}}{2} &\therefore& \lambda_{ii} =68 \cdot 10^{-2} \ \pu{m}
\end{matrix}Portanto, conforme equação fundamental da ondulatória:\begin{matrix}
v_{som} = \lambda_{ii} f_{ii} &\therefore& \boxed{f_{ii} = 500 \ \pu{Hz}}
\end{matrix}\begin{matrix}Letra \ (C)
\end{matrix}
Observe que há uma diferença entre os comprimentos, e esta diferença será responsável pelos resultados distintos das frequências. Nesse sentido, encontrar $\overline{AB}$ não é difícil, visto que:\begin{matrix}
\overline{AB} +\overline{BD} = \overline{AD}
\end{matrix}Consequentemente,\begin{matrix}
2 \overline{AB} = 34 &\therefore& \overline{AB} = 17 \cdot 10^{-2} \ \pu{m}
\end{matrix}Pensando no comprimento de onda do caso $(i)$, têm-se:\begin{matrix}
\overline{AB} = \dfrac{\lambda_i}{2} &\therefore& \lambda_i =34 \cdot 10^{-2} \ \pu{m}
\end{matrix}Conforme equação fundamental da ondulatória:\begin{matrix}
v_{som} = \lambda_i f_{i} &\therefore& \boxed{ f_{i} = 1000 \ \pu{Hz}}
\end{matrix}Por outro lado, para o caso $(ii)$:\begin{matrix}
\overline{AD} = \dfrac{\lambda_{ii}}{2} &\therefore& \lambda_{ii} =68 \cdot 10^{-2} \ \pu{m}
\end{matrix}Portanto, conforme equação fundamental da ondulatória:\begin{matrix}
v_{som} = \lambda_{ii} f_{ii} &\therefore& \boxed{f_{ii} = 500 \ \pu{Hz}}
\end{matrix}\begin{matrix}Letra \ (C)
\end{matrix}

Ampliar Imagem

