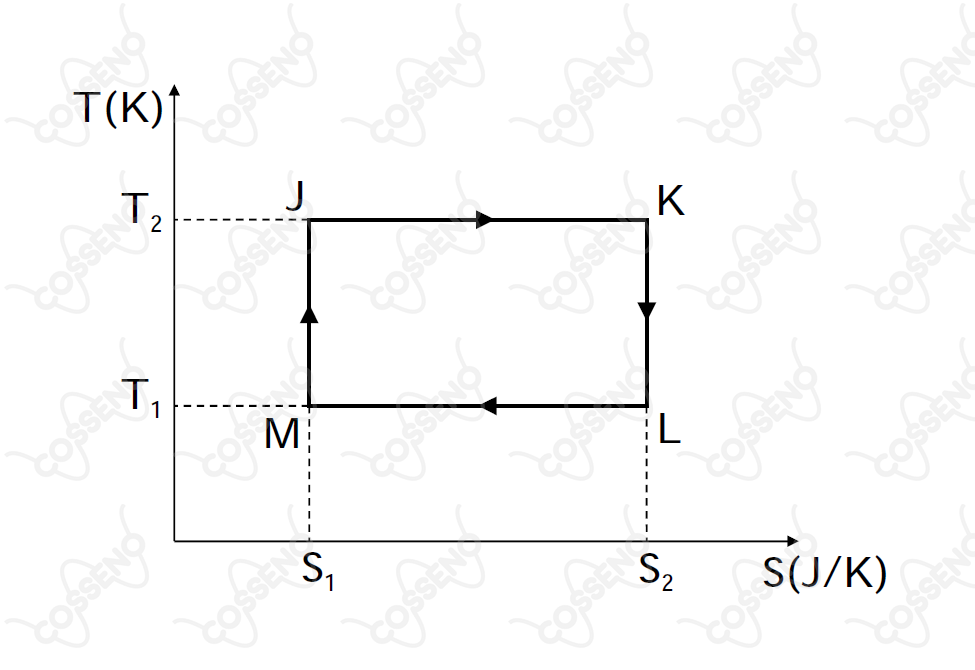
Uma maquina térmica opera segundo o ciclo JKLMJ mostrado no diagrama T-S da figura. Pode-se afirmar que
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A princípio, observe que o ciclo compreende dois processos isotérmicos (uma expansão e uma compressão), assim como dois processos isentrópicos - entalpia constante - que consequentemente conferem dois processos adiabáticos (uma expansão e uma compressão), ou seja, o ciclo em questão é de $\text{Carnot}$. Nesse sentido, vamos avaliar as alternativas:
$• \ \text{Alternativa (A):}$ $\color{orangered}{\text{Incorreta}}$
Na verdade, ele corresponde a uma $\text{expansão}$ isotérmica.
$• \ \text{Alternativa (B):}$ $\color{#3368b8}{\text{Correta}}$
O trabalho do ciclo equivale a área interna do mesmo, ou seja:\begin{matrix}
W \overset{N}{=} (T_2 -T_1)(S_2 - S_1)
\end{matrix}$\color{orangered}{\text{Obs:}}$ Você pode conferir este resultando calculando o trabalho realizado por cada processo a partir do conceito de entalpia junto a primeira lei da termodinâmica. Após isso, basta somar algebricamente os resultados e verificar a preposição acima.
$• \ \text{Alternativa (C):}$ $\color{orangered}{\text{Incorreta}}$
Como o ciclo é de Carnot, o rendimento pode ser calculado como:\begin{matrix}
\eta = 1 - \dfrac{T_{fria}}{T_{quente}}
\end{matrix}Por outro lado, pelo gráfico, nota-se que $T_2 = T_{quente}$ e $T_1 = T_{fria}$. Consequentemente, o rendimento exposto pela alternativa não condiz com o ciclo de Carnot.
$• \ \text{Alternativa (D):}$ $\color{orangered}{\text{Incorreta}}$
O processo $LM$ é uma compressão isotérmica, ou seja, é realizado trabalho sobre o sistema, logo, a energia de agitação das moléculas tende a aumentar - consequentemente, a temperatura também. Todavia, o processo é isotérmico, o que confere que o sistema $\text{cede calor}$ durante a compressão $LM$ a fim de manter a temperatura constante.
$• \ \text{Alternativa (E):}$ $\color{orangered}{\text{Incorreta}}$
Não, pois, por definição, o rendimento máximo é a partir da máquina de Carnot.\begin{matrix}Letra \ (B)
\end{matrix}

