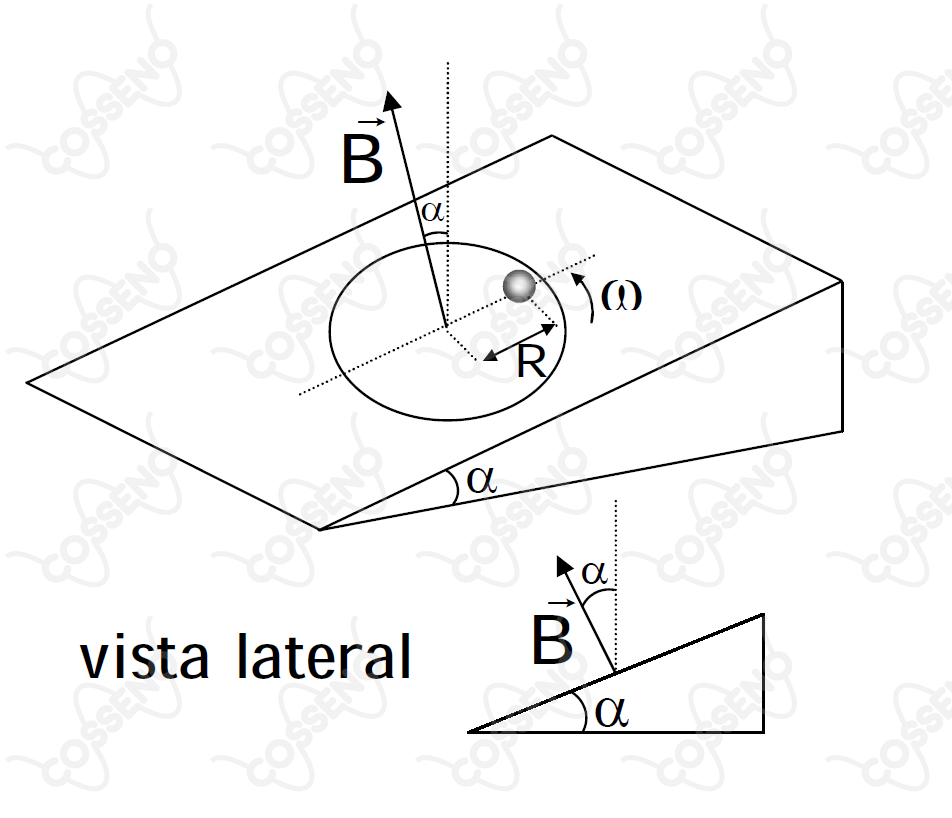
Um disco, com o eixo de rotação inclinado de um ângulo em relação à vertical, gira com velocidade angular constante. O disco encontra-se imerso numa região do espaço onde existe um campo magnético uniforme e constante, orientado paralelamente ao eixo de rotação do disco. Uma partícula de massa e carga encontra-se no plano do disco, em repouso em relação a este, e situada a uma distância do centro, conforme a figura. Sendo o coeficiente de atrito da partícula com o disco e a aceleração da gravidade, determine até que valor de o disco pode girar de modo que a partícula permaneça em repouso.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Pela geometria plana, o ângulo que $\vec{B}$ faz com o plano inclinado é reto (na prova, obviamente o candidato teria que mostrar isso). Assim, sabendo que a partícula está em equilíbrio e na iminência do movimento, pela $2°$ Lei de Newton, temos que$$qwRB + mw^2R + mg\sin \alpha~=~\mu mg\cos \alpha$$Logo$$mR\cdot w^2+qRB\cdot w - mg(\mu\cos \alpha - \sin \alpha)~=~0$$Resolvendo a equação quadrática em $w > 0$, concluí-se que$$\boxed{w~=~\dfrac{-qRB+\sqrt{q^2R^2B^2+4m^2Rg(\mu\cos \alpha - \sin \alpha)}}{2mR}}$$

