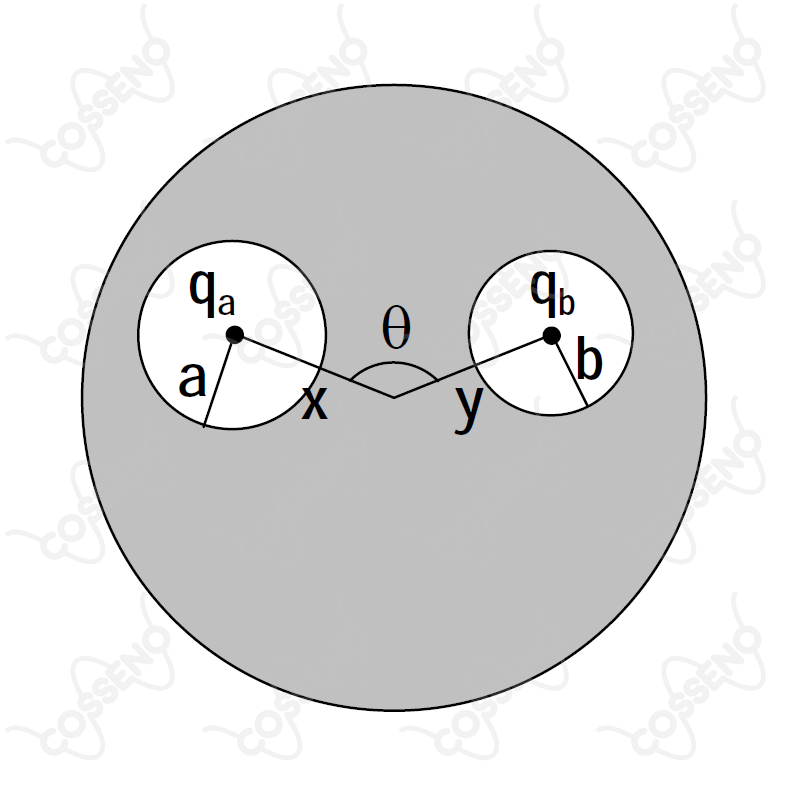
Uma esfera condutora de raio possui no seu interior duas cavidades esféricas, de raio e , respectivamente, conforme mostra a figura. No centro de uma cavidade há uma carga pontual e no centro da outra, uma carga também pontual , cada qual distando do centro da esfera condutora de e , respectivamente. É correto afirmar que
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A princípio, a questão trata sobre os conceitos de $\text{indução total}$ e $\text{blindagem eletrostática}$. No caso, observe que as cargas nas cavidades irão induzir cargas opostas ao redor das cavidades, e estas por sua vez irão promover cargas opostas na superfície do condudor. Nesse sentido, temos a indução total, em que conforme princípio da conservação de cargas, têm-se para o condutor:\begin{matrix}
Q_{condutor} = q_a + q_b
\end{matrix}Por outro lado, o ponto da questão não é esse em si, mas o resultado que provém dele, isto é, a blindagem que ocorre. Em suma, as cargas estão isoladas, não há campo elétrico interno algum devido a blindagem (assim como por o corpo ser um condutor), portanto, a força entre as cargas é nula - se não há campo elétrico, não há força elétrica. Analisando as alternativas:
$• \ \text{Alternativas (A) e (C):}$ $\color{orangered}{\text{Incorretas}}$
Vide análise anterior.
$• \ \text{Alternativa (B):}$ $\color{#3368b8}{\text{Correta}}$
Vide análise anterior.
$• \ \text{Alternativas (D):}$ $\color{orangered}{\text{Incorretas}}$
O condutor pode apresentar carga, e este deve produzir um campo magnético saindo do condutor, logo, uma carga nas proximidades sofreria interação elétrica.
$• \ \text{Alternativas (E):}$ $\color{orangered}{\text{Incorretas}}$
Não seria alterada pois a carga estaria externa ao sistema, não produzindo qualquer alteração de fluxo, conforme $\text{Lei de Gauss}$.\begin{matrix}Letra (B)
\end{matrix}

