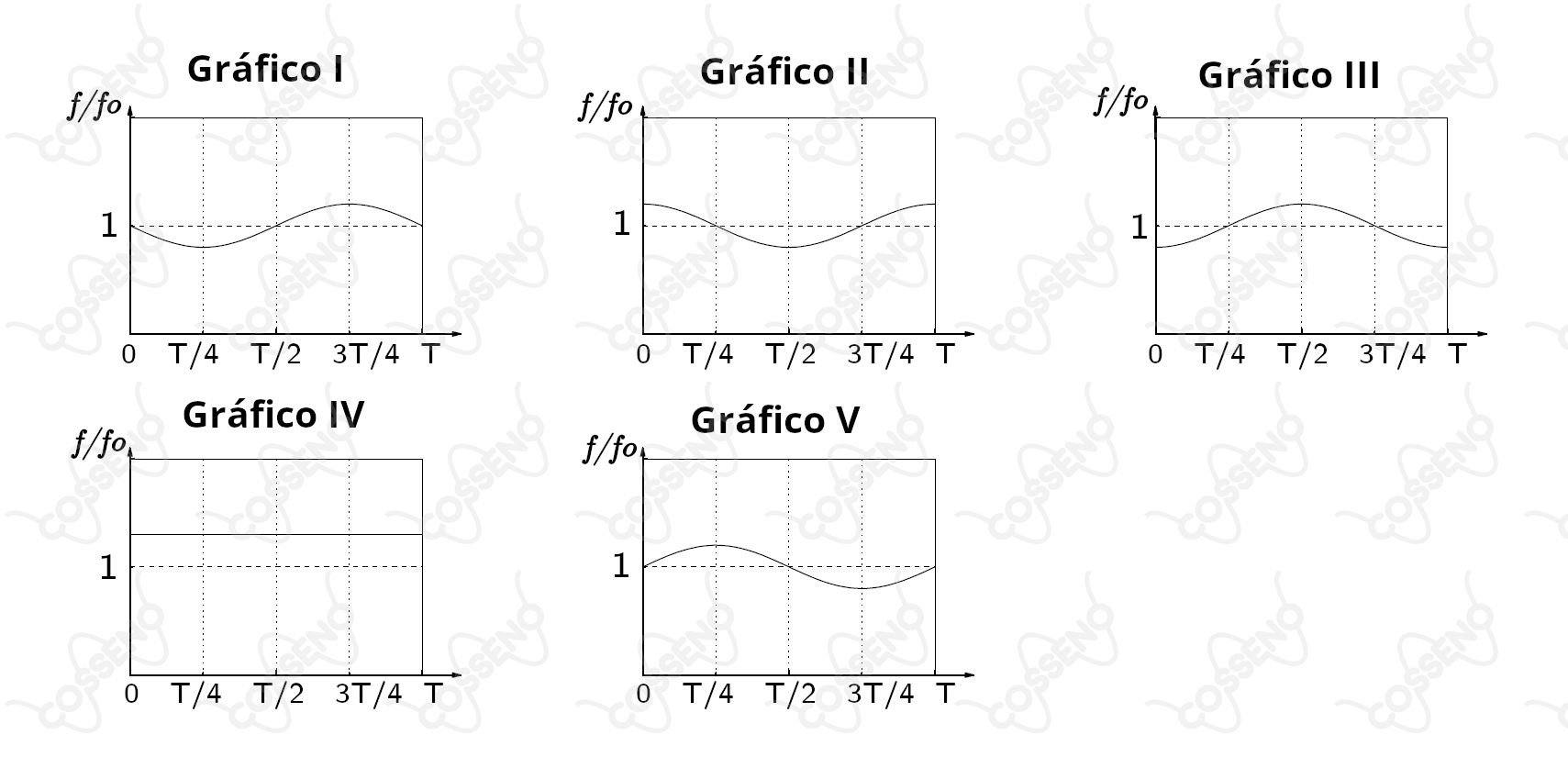
Uma jovem encontra-se no assento de um carrossel circular que gira a uma velocidade angular constante com período . Uma sirene posicionada fora do carrossel emite um som de frequência em direcão ao centro de rotação. No instante , a jovem está à menor distância em relação à sirene. Nesta situação, assinale a melhor representação da frequência ouvida pela jovem.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Pensando na situação descrita, podemos esboçar a partir de uma visão superior do carrossel:
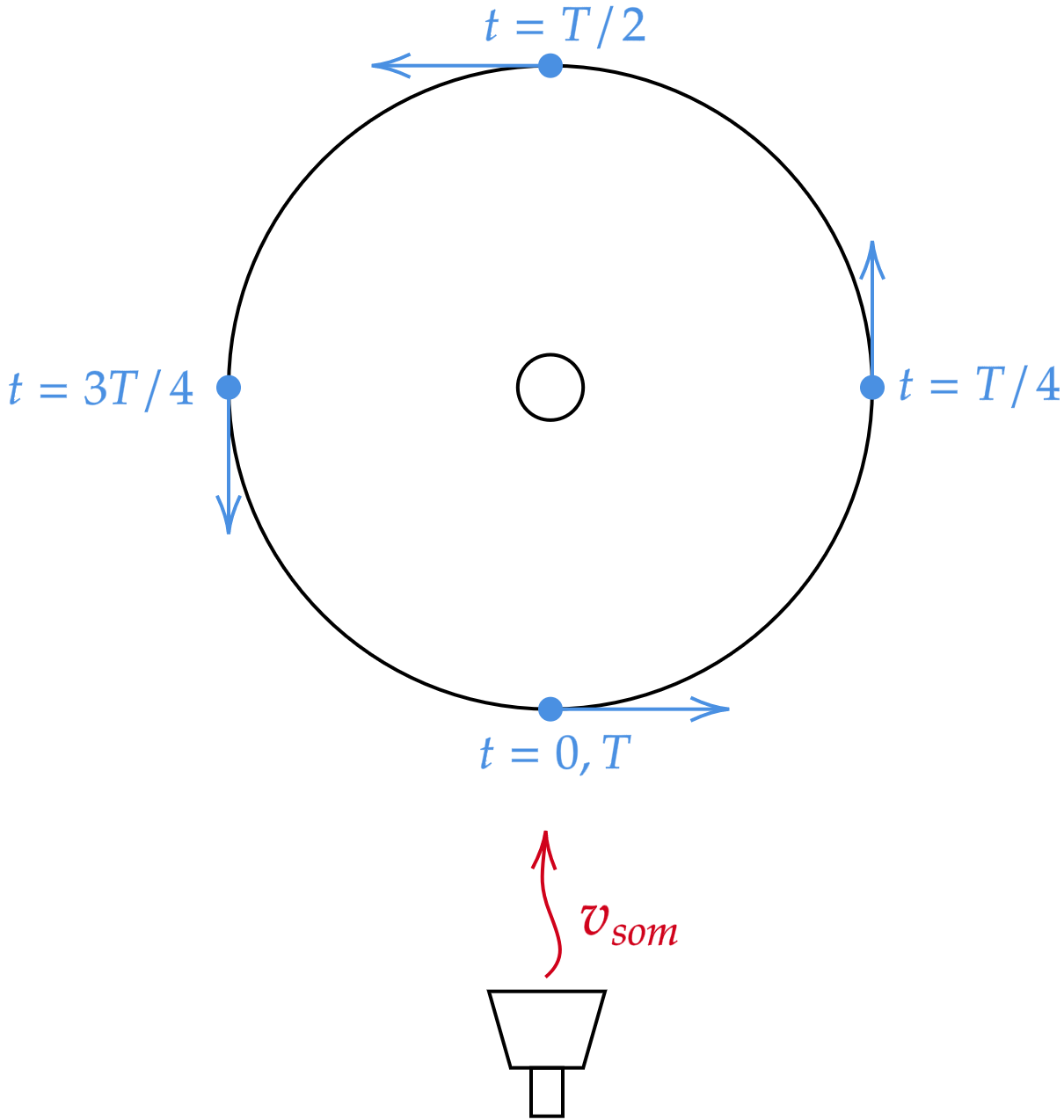 Nesse sentido, a questão se restringe ao conhecimento qualitativo do $\text{efeito Doppler}$. No caso, observe que a fonte é imóvel, então a análise se baseia no movimento do jovem (observador), tal que a equação pode ser descrita como:\begin{matrix}
\dfrac{f}{f_0} = \dfrac{v_{som} \pm v_{ob}}{v_{som}}
\end{matrix}Dessa forma vamos analisar os momentos:
$• \ \text{Instantes t = 0 e t = T/2:}$ $\color{#3368b8}{\dfrac{f}{f_0} = 1}$
Pondere que em ambos os instantes a velocidade relativa do objeto é perpendicular à do som, ou seja, não há velocidade relativa. Portanto, a frequência percebida pelo jovem é a mesma que a da fonte.
$• \ \text{Instante t = T/4:}$ $\color{#3368b8}{\dfrac{f}{f_0} < 1}$
Repare que o jovem está se afastando da fonte paralelamente à esta, ou seja, ele irá ouvir um som mais grave, consequentemente, de menor frequência. Em termos quantitativos, há a fórmula abaixo:\begin{matrix}
\dfrac{f}{f_0} = \dfrac{v_{som} - v_{ob}}{v_{som}}
\end{matrix}$• \ \text{Instante t = 3T/4:}$ $\color{#3368b8}{\dfrac{f}{f_0} < 1}$
Conforme análise anterior, note que a diferença entre os dois instantes se concentra no sentido do movimento, isto é, agora, o jovem está se aproximando da fonte. Desse modo, o som que o observador irá ouvir será mais agudo, quer dizer, a frequência recebida será maior, vide equação abaixo:\begin{matrix}
\dfrac{f}{f_0} = \dfrac{v_{som} + v_{ob}}{v_{som}}
\end{matrix}\begin{matrix}Letra \ (A)
\end{matrix}
Nesse sentido, a questão se restringe ao conhecimento qualitativo do $\text{efeito Doppler}$. No caso, observe que a fonte é imóvel, então a análise se baseia no movimento do jovem (observador), tal que a equação pode ser descrita como:\begin{matrix}
\dfrac{f}{f_0} = \dfrac{v_{som} \pm v_{ob}}{v_{som}}
\end{matrix}Dessa forma vamos analisar os momentos:
$• \ \text{Instantes t = 0 e t = T/2:}$ $\color{#3368b8}{\dfrac{f}{f_0} = 1}$
Pondere que em ambos os instantes a velocidade relativa do objeto é perpendicular à do som, ou seja, não há velocidade relativa. Portanto, a frequência percebida pelo jovem é a mesma que a da fonte.
$• \ \text{Instante t = T/4:}$ $\color{#3368b8}{\dfrac{f}{f_0} < 1}$
Repare que o jovem está se afastando da fonte paralelamente à esta, ou seja, ele irá ouvir um som mais grave, consequentemente, de menor frequência. Em termos quantitativos, há a fórmula abaixo:\begin{matrix}
\dfrac{f}{f_0} = \dfrac{v_{som} - v_{ob}}{v_{som}}
\end{matrix}$• \ \text{Instante t = 3T/4:}$ $\color{#3368b8}{\dfrac{f}{f_0} < 1}$
Conforme análise anterior, note que a diferença entre os dois instantes se concentra no sentido do movimento, isto é, agora, o jovem está se aproximando da fonte. Desse modo, o som que o observador irá ouvir será mais agudo, quer dizer, a frequência recebida será maior, vide equação abaixo:\begin{matrix}
\dfrac{f}{f_0} = \dfrac{v_{som} + v_{ob}}{v_{som}}
\end{matrix}\begin{matrix}Letra \ (A)
\end{matrix}

Ampliar Imagem

