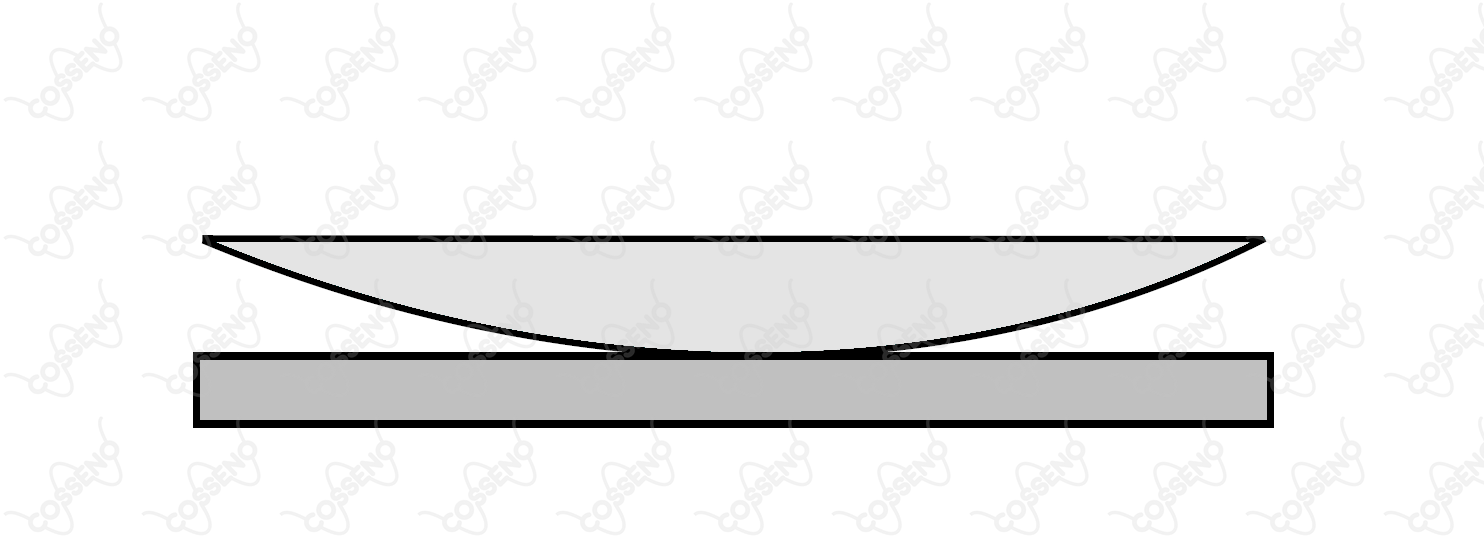
Um feixe luminoso vertical, de de comprimento de onda, incide sobre uma lente plano-convexa apoiada numa lâmina horizontal de vidro, como mostra a figura. Devido à variação da espessura da camada de ar existente entre a lente e a lâmina, torna-se visível sobre a lente uma sucessão de anéis claros e escuros, chamados de anéis de Newton. Sabendo-se que o diâmetro do menor anel escuro mede , a superfície convexa da lente deve ter um raio de
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A princípio, pode-se esboçar a situação para um raio $r$ de um k-ésimo anel escuro qualquer:
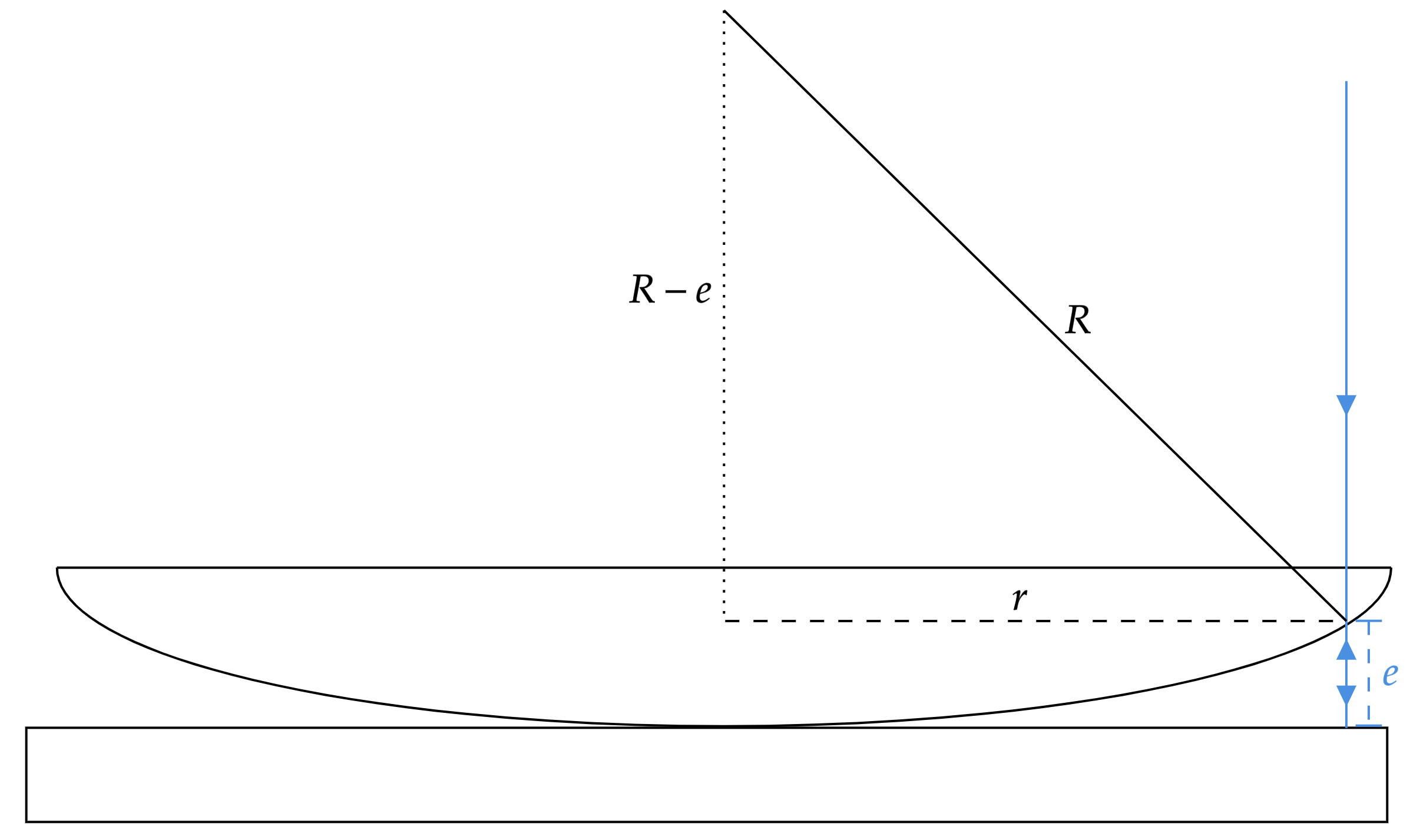 Observe que $R$ é o raio da superfície convexa, assim como $e$ a espessura da camada de ar existente entre a lâmina e a lente. Nesse sentido, comecemos por pensar na interferência, como estamos falando de um anel escuro, esta deve ser destrutiva. Além disso, repare que os raios estão em oposição de fase, visto que o raio refletido pela lâmina horizontal provém de um meio com menor índice de refração que a mesma. Com isso, para diferença de caminho óptico, temos:\begin{matrix} 2e = k \lambda
\end{matrix}$\color{orangered}{\text{Obs:}}$ Pela imagem acima pode ser difícil perceber, mas a diferença está, aproximadamente, em $2e$, visto que o raio é transmitido pela lente - percorre-se $e$ - e volta pela reflexão da lâmina - percorrendo mais $e$.
Como estamos falando do menor anel escuro, certamente visamos a menor diferença de comprimento de onda, isto é, $k = 1$. Dessa forma, substituindo os dados do enunciado, têm-se:\begin{matrix}
e = \dfrac{500 \cdot 10^{-9}}{2} &\therefore& e = 250 \cdot 10^{-9} \ \pu{m}
\end{matrix}Por fim, resta-nos aplicar o teorema de Pitágoras no triângulo da imagem:\begin{matrix}
R^2 = (R-e)^2 + r^2 &,& r = 1 \cdot 10^{-3} \ \pu{m}
\end{matrix}Pondere que $e$ é muito menor que $R$ e $r$, consequentemente, o termo $e^2$ é desprezível, restando apenas:\begin{matrix}
2Re = r^2 &\Rightarrow& R = \dfrac{(1\cdot 10^{-3})^2}{2 (250 \cdot 10^{-9})} &\therefore& R = 2,0 \ \pu{m} \ \ \ \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (C)
\end{matrix}
Observe que $R$ é o raio da superfície convexa, assim como $e$ a espessura da camada de ar existente entre a lâmina e a lente. Nesse sentido, comecemos por pensar na interferência, como estamos falando de um anel escuro, esta deve ser destrutiva. Além disso, repare que os raios estão em oposição de fase, visto que o raio refletido pela lâmina horizontal provém de um meio com menor índice de refração que a mesma. Com isso, para diferença de caminho óptico, temos:\begin{matrix} 2e = k \lambda
\end{matrix}$\color{orangered}{\text{Obs:}}$ Pela imagem acima pode ser difícil perceber, mas a diferença está, aproximadamente, em $2e$, visto que o raio é transmitido pela lente - percorre-se $e$ - e volta pela reflexão da lâmina - percorrendo mais $e$.
Como estamos falando do menor anel escuro, certamente visamos a menor diferença de comprimento de onda, isto é, $k = 1$. Dessa forma, substituindo os dados do enunciado, têm-se:\begin{matrix}
e = \dfrac{500 \cdot 10^{-9}}{2} &\therefore& e = 250 \cdot 10^{-9} \ \pu{m}
\end{matrix}Por fim, resta-nos aplicar o teorema de Pitágoras no triângulo da imagem:\begin{matrix}
R^2 = (R-e)^2 + r^2 &,& r = 1 \cdot 10^{-3} \ \pu{m}
\end{matrix}Pondere que $e$ é muito menor que $R$ e $r$, consequentemente, o termo $e^2$ é desprezível, restando apenas:\begin{matrix}
2Re = r^2 &\Rightarrow& R = \dfrac{(1\cdot 10^{-3})^2}{2 (250 \cdot 10^{-9})} &\therefore& R = 2,0 \ \pu{m} \ \ \ \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (C)
\end{matrix}

Ampliar Imagem

