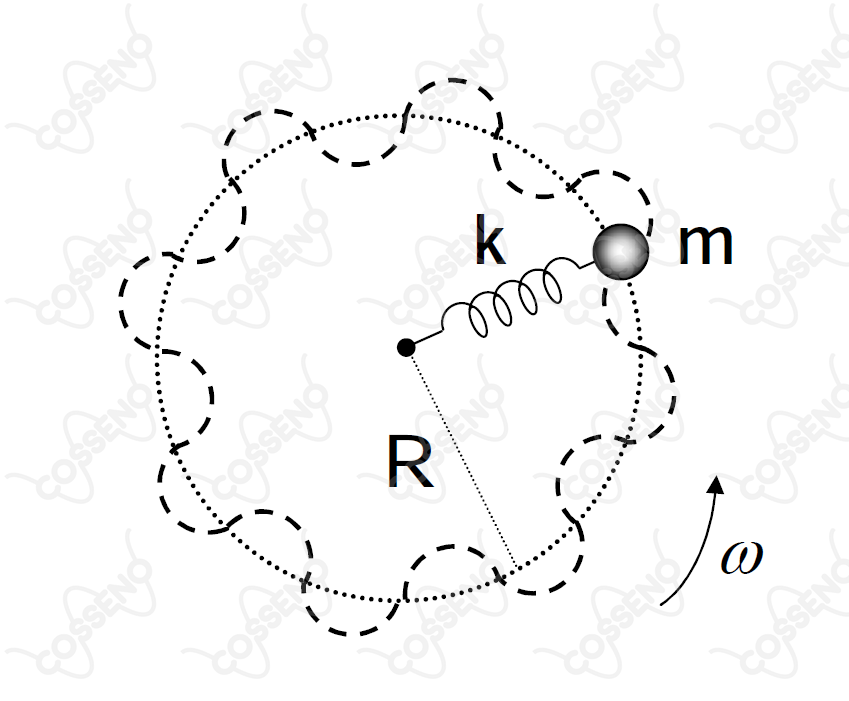
Considere um oscilador harmônico simples composto por uma mola de constante elástica , tendo uma extremidade fixada e a outra acoplada a uma partícula de massa . O oscilador gira num plano horizontal com velocidade angular constante em torno da extremidade fixa, mantendo-se apenas na direção radial, conforme mostra a figura. Considerando a posição de equilíbrio do oscilador para , pode-se afirmar que
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Ao ler a questão, já nos deparamos com um sistema bem conhecido: massa e mola que giram em torno de um eixo fixo.
Mas o enunciado ainda fala que existe um MHS - e talvez não esteja claro qual é a origem exata dessa oscilação.
Se a massa estiver girando, a única coisa que acontece com a mola é uma distensão - ela aumenta de comprimento por causa da componente centrípeta - e permanece rodando em equilíbrio.
$\text{Onde está o MHS?}$
Como a figura do enunciado sugere, devemos assumir que há uma pequena perturbação, que provoca deslocamento do ponto de equilíbrio!
O caso mais simples ocorre com $\omega=0$.
Aqui, é só um sistema massa-mola que oscila harmonicamente em torno do comprimento natural $R_0$ da mola.
Mas agora, quando já temos a massa rodando e então fazemos uma perturbação, o caminho que a massa faz durante esse MHS é justamente essa linha tracejada que o enunciado mostra.
A maior diferença aqui vai ser a posição de equilíbrio:
Ao aumentar o ômega, a mola tende a aumentar de comprimento (sair pela tangente). Ela só não aumenta infinitamente porque a força elástica "puxa" a massa para o centro, o acompanhando o movimento da curva. Essa e á origem da resultante centrípeta!
Para descobrir o comprimento da mola $R_E$ durante esse movimento circular, nesta nova posição de equilíbrio, basta igualar a força elástica à resultante centrípeta:$$k(R_E - R_0) = m\omega^2R_E\\\boxed{R_E = \frac{kR_0}{k - m\omega^2}}$$
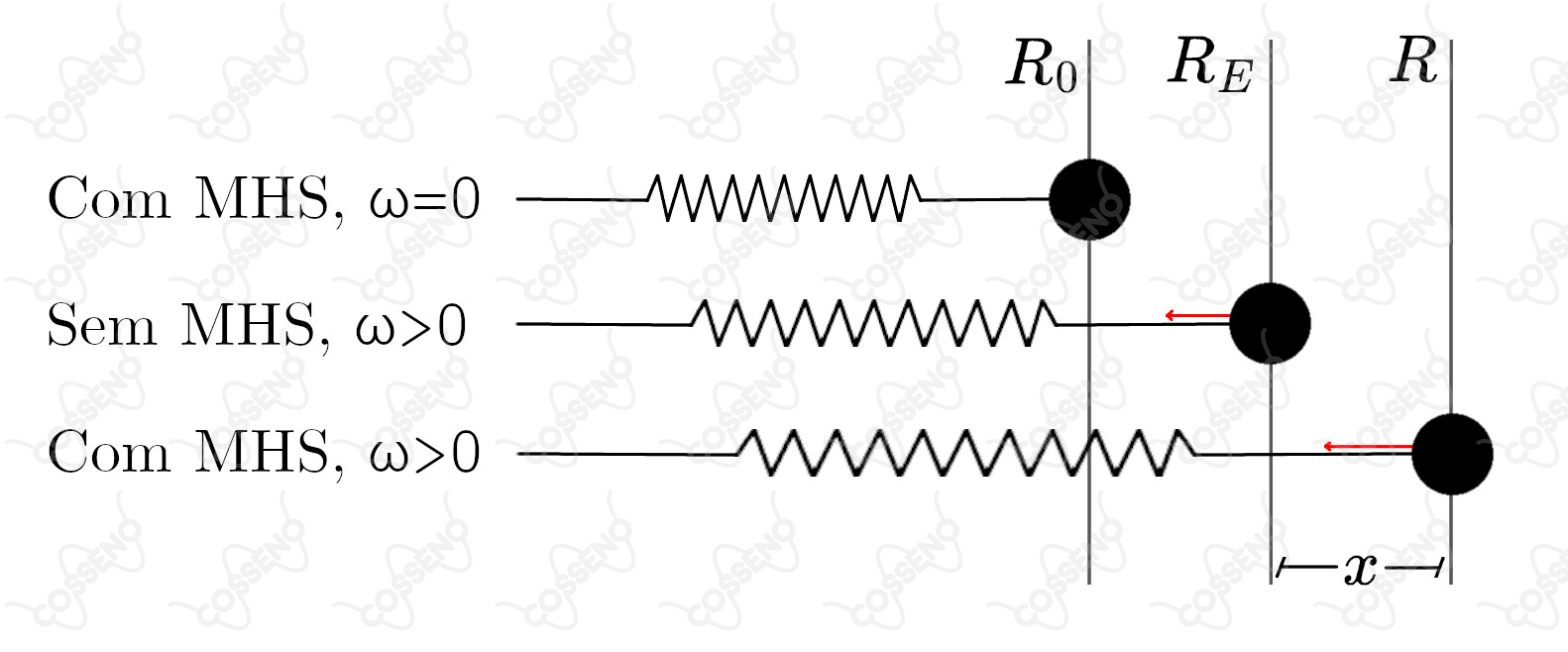 Mas agora, após a perturbação, o MHS faz o comprimento da mola variar - de modo que o raio do movimento será $R$, que depende diretamente do deslocamento $x$ em relação à posição de equilíbrio $R_E$, conforme imagem acima.
Lembrando que, na situação de equilíbrio, a força elástica é igual à resultante centrípeta:$$m\omega^2 R_E=k (R_E - R_0)\quad\text{[Eq. 1]}$$Já durante o MHS, a aceleração resultante será igual à centrípeta - permitindo que a massa faz a curva - SOMADA à aceleração do MHS - que puxa a massa de volta para a posição de equilíbrio $R_E$. Ou seja, sendo $a$ a aceleração do MHS:$$m\omega^2 R=k(R - R_0) - ma$$E como $R=R_E+x$ (ver figura):$$m\omega^2 (R_E + x)=k(R_E + x - R_E)-ma\\ m\omega^2 R_E + m\omega^2 x = k (R_E - R_0)+kx-ma$$Recorrendo à $\text{[Eq. 1]}$ para cancelar o primeiro termo de cada membro, ficamos com:$$ma=kx-m\omega^2x$$Aqui identificamos a equação característica do MHS:$$a=\left(\frac{k}{m} - \omega^2\right) x$$Fazendo com que a frequência do MHS seja:$$\boxed{f=\frac{1}{2\pi}\sqrt{\frac{k}{m}-\omega^2}}$$Enfim, tendo entendido a situação, vamos às alternativas:
$\textbf{a) FALSO}$ - Com $\omega=\sqrt{\frac{k}{m}}$, segue que $f=0$, fazendo com que não exista oscilação. Só existe MHS para $\omega^2<\frac{k}{m}$.
$\textbf{b) FALSO}$ - Conforme determinamos anteriormente, o valor máximo de $R_E$ ocorre quando $\omega=0$, fazendo com que o equilíbrio seja deslocado para $R_E>R_0$ quando ocorre rotação.
$\textbf{c) FALSO}$ - da expressão que encontramos para $f(\omega)$, é evidente que $\omega=0$ garante $f$ máximo.
$\textbf{d) VERDADEIRO}$ - basta notar que $(f(\omega))^2=\frac{1}{4\pi^2}\left(\frac{k}{m}-\omega^2\right)$, ficando assim evidente a dependência linear entre $f^2$ e $\omega^2$.
$\textbf{e) FALSO}$ - havendo campo magnético na direção do eixo, podemos determinar - com a regra da mão direita - que surgirá uma força magnética no sentido radial - para "dentro" ou "fora" dependendo do sinal da carga. Isso altera a posição de equilíbrio, como se tivéssemos alterado a constante elástica da mola, de modo que uma força "para fora" faz com que $R_E$ aumente. Assim, $\omega=2\pi f$ diminui - isto é - há redução na frequência do MHS.
$$\boxed{\text{Gab. D)}}$$
Mas agora, após a perturbação, o MHS faz o comprimento da mola variar - de modo que o raio do movimento será $R$, que depende diretamente do deslocamento $x$ em relação à posição de equilíbrio $R_E$, conforme imagem acima.
Lembrando que, na situação de equilíbrio, a força elástica é igual à resultante centrípeta:$$m\omega^2 R_E=k (R_E - R_0)\quad\text{[Eq. 1]}$$Já durante o MHS, a aceleração resultante será igual à centrípeta - permitindo que a massa faz a curva - SOMADA à aceleração do MHS - que puxa a massa de volta para a posição de equilíbrio $R_E$. Ou seja, sendo $a$ a aceleração do MHS:$$m\omega^2 R=k(R - R_0) - ma$$E como $R=R_E+x$ (ver figura):$$m\omega^2 (R_E + x)=k(R_E + x - R_E)-ma\\ m\omega^2 R_E + m\omega^2 x = k (R_E - R_0)+kx-ma$$Recorrendo à $\text{[Eq. 1]}$ para cancelar o primeiro termo de cada membro, ficamos com:$$ma=kx-m\omega^2x$$Aqui identificamos a equação característica do MHS:$$a=\left(\frac{k}{m} - \omega^2\right) x$$Fazendo com que a frequência do MHS seja:$$\boxed{f=\frac{1}{2\pi}\sqrt{\frac{k}{m}-\omega^2}}$$Enfim, tendo entendido a situação, vamos às alternativas:
$\textbf{a) FALSO}$ - Com $\omega=\sqrt{\frac{k}{m}}$, segue que $f=0$, fazendo com que não exista oscilação. Só existe MHS para $\omega^2<\frac{k}{m}$.
$\textbf{b) FALSO}$ - Conforme determinamos anteriormente, o valor máximo de $R_E$ ocorre quando $\omega=0$, fazendo com que o equilíbrio seja deslocado para $R_E>R_0$ quando ocorre rotação.
$\textbf{c) FALSO}$ - da expressão que encontramos para $f(\omega)$, é evidente que $\omega=0$ garante $f$ máximo.
$\textbf{d) VERDADEIRO}$ - basta notar que $(f(\omega))^2=\frac{1}{4\pi^2}\left(\frac{k}{m}-\omega^2\right)$, ficando assim evidente a dependência linear entre $f^2$ e $\omega^2$.
$\textbf{e) FALSO}$ - havendo campo magnético na direção do eixo, podemos determinar - com a regra da mão direita - que surgirá uma força magnética no sentido radial - para "dentro" ou "fora" dependendo do sinal da carga. Isso altera a posição de equilíbrio, como se tivéssemos alterado a constante elástica da mola, de modo que uma força "para fora" faz com que $R_E$ aumente. Assim, $\omega=2\pi f$ diminui - isto é - há redução na frequência do MHS.
$$\boxed{\text{Gab. D)}}$$

Ampliar Imagem


