Considere a Terra como uma esfera homogênea de raio que gira com velocidade angular uniforme em torno do seu próprio eixo Norte-Sul. Na hipótese de ausência de rotação da Terra, sabe-se que a aceleração da gravidade seria dada por . Como , um corpo em repouso na superfície da Terra na realidade fica sujeito forçosamente a um peso aparente, que pode ser medido, por exemplo, por um dinamômetro, cuja direção pode não passar pelo centro do planeta. Então, o peso aparente de um corpo de massa em repouso na superfície da Terra a uma latitude é dado por

CossenoGPT
Teste
gratuitamente agora
mesmo! 

Analisando as forças que atuam no corpo, nota-se a força gravitacional $\vec{F}_G$, a resultante centrípeta $\vec{F}_{cp}$ e a reação de contato entre o objeto e o solo. Nesse sentido, a composição da força gravitacional junto a resultante centrípeta deve promover o peso aparente $\vec{P}_{ap}$, o que pode ser visualizado baixo:
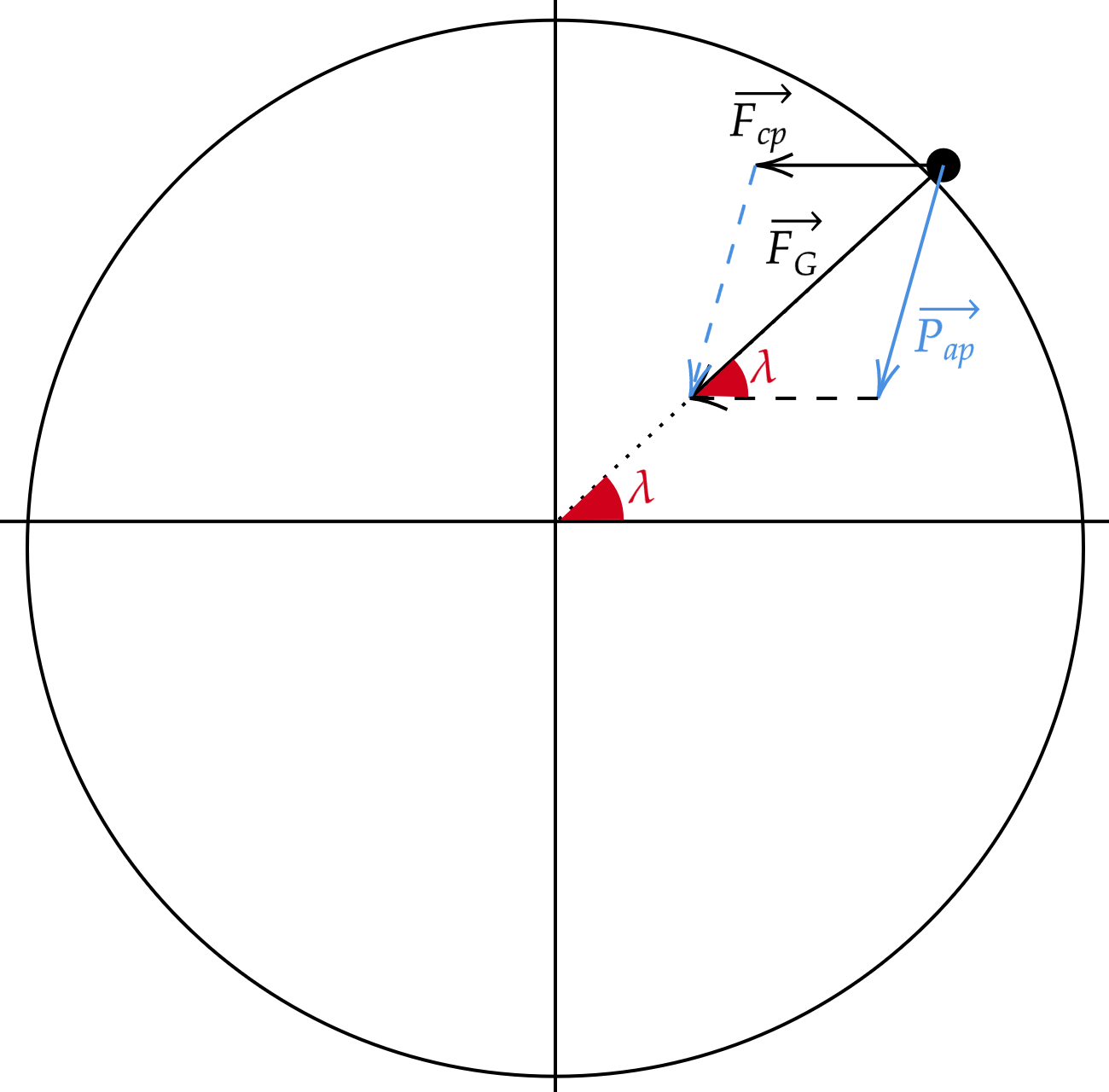 Aplicando a lei dos cossenos, facilmente constatamos:\begin{matrix}
|\vec{P}_{ap}|^2 = |\vec{F}_{cp}|^2 + |\vec{F}_{G}|^2 - 2 |\vec{F}_{cp}||\vec{F}_{G}|\cos{\lambda}
\end{matrix}Consequentemente,\begin{matrix}
|\vec{P}_{ap}|^2 = (mg)^2 + (m\omega^2r)^2 -2(mg)(m\omega^2r)\cos{\lambda}
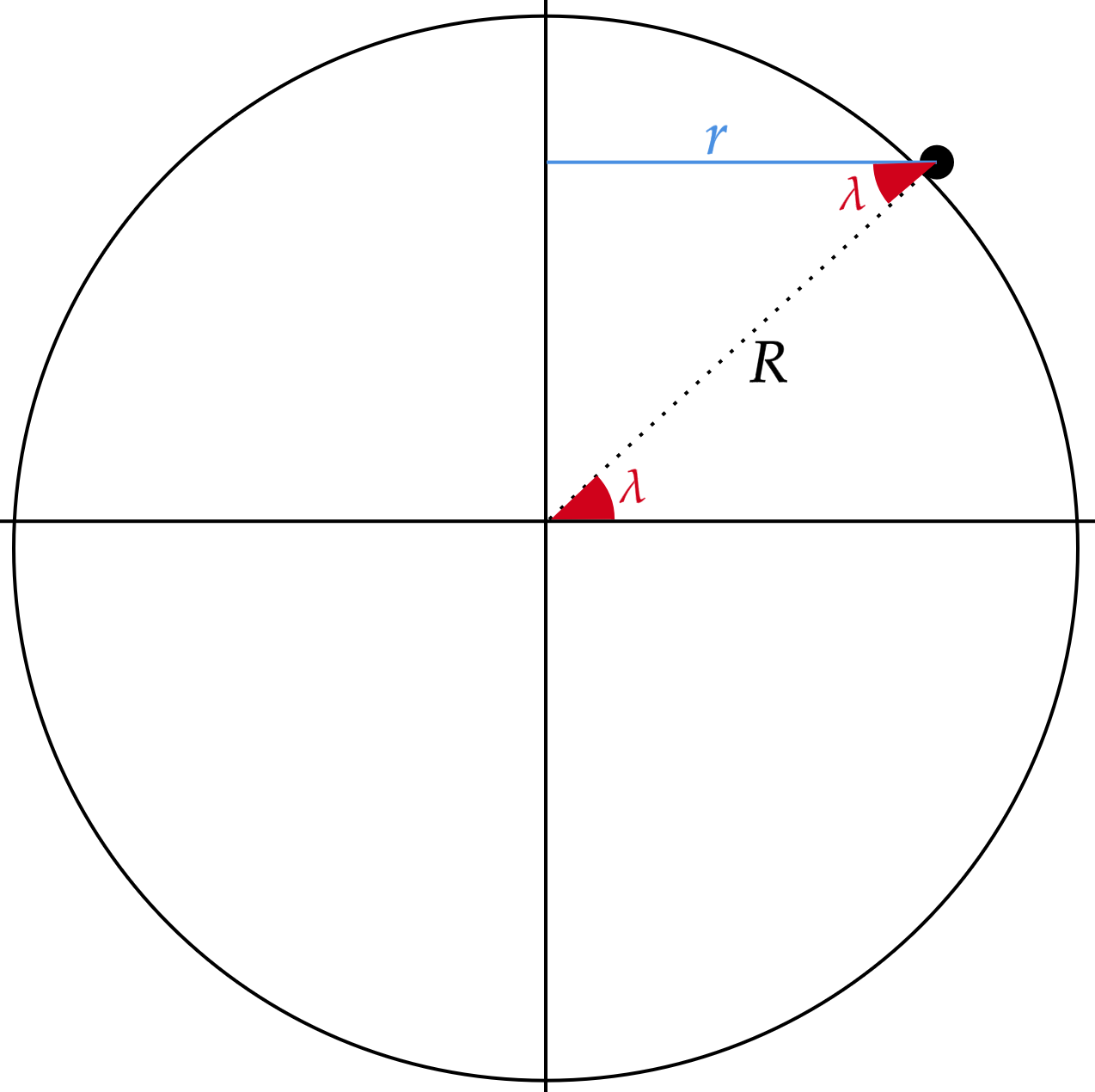
\end{matrix}Encontrar $r$ não é difícil, veja:\begin{matrix}r = R \cos{\lambda}
\end{matrix}
Aplicando a lei dos cossenos, facilmente constatamos:\begin{matrix}
|\vec{P}_{ap}|^2 = |\vec{F}_{cp}|^2 + |\vec{F}_{G}|^2 - 2 |\vec{F}_{cp}||\vec{F}_{G}|\cos{\lambda}
\end{matrix}Consequentemente,\begin{matrix}
|\vec{P}_{ap}|^2 = (mg)^2 + (m\omega^2r)^2 -2(mg)(m\omega^2r)\cos{\lambda}
\end{matrix}Encontrar $r$ não é difícil, veja:\begin{matrix}r = R \cos{\lambda}
\end{matrix}
 Portanto,\begin{matrix}
|\vec{P}_{ap}| = mg \sqrt{1 - \left[\dfrac{2\omega^2R}{g} - \left(\dfrac{\omega^2R}{g}\right)^{2}\right ]\cos^2{\lambda}}
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}
Portanto,\begin{matrix}
|\vec{P}_{ap}| = mg \sqrt{1 - \left[\dfrac{2\omega^2R}{g} - \left(\dfrac{\omega^2R}{g}\right)^{2}\right ]\cos^2{\lambda}}
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}

Ampliar Imagem

Ampliar Imagem

