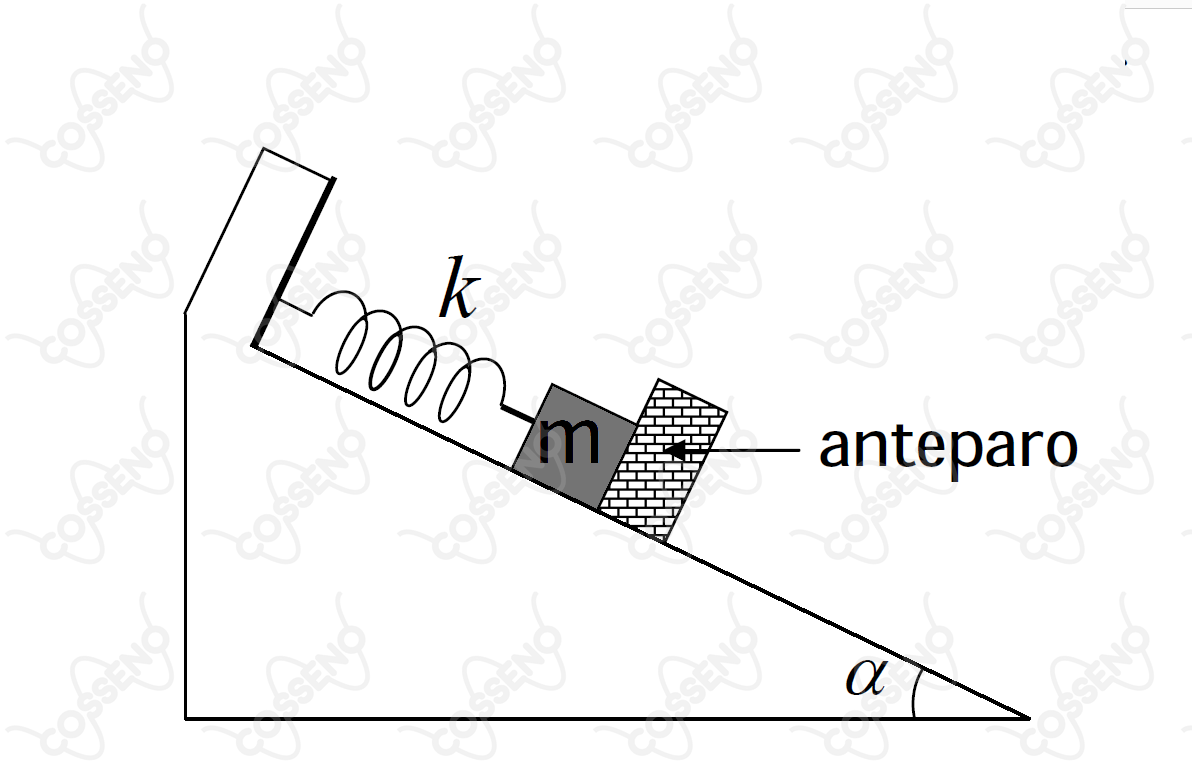
No plano inclinado, o corpo de massa é preso a uma mola de constante elástica , sendo barrado a frente por um anteparo. Com a mola no seu comprimento natural, o anteparo, de alguma forma, inicia seu movimento de descida com uma aceleração constante . Durante parte dessa descida, o anteparo mantém contato com o corpo, dele se separando somente após um certo tempo. Desconsiderando quaisquer atritos, podemos afirmar que a variação máxima do comprimento da mola é dada por
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A princípio, analisando o movimento do bloco junto ao anteparo, pode-se inferir que durante este movimento ambos possuirão a mesma aceleração $\vec{a}$, visto que o movimento do bloco é, neste período, ligado do anteparo. Nesse contexto, analisando as forças que atuam no bloco, temos:\begin{matrix}
ma = mg\sin{\alpha} - kx &\therefore&x = \dfrac{m(g\sin{\alpha} - a)}{k}
\end{matrix}O ponto aqui é que este movimento acima deve ocorrer até uma determinada distância que chamaremos de $x_1$, esta que não deve compreender a deformação máxima de mola. Analogamente, vamos assumir que a deformação máxima da mola ocorra em $x_2$, sabemos que a equação anterior não varre $x_2$, conduto, a conservação da energia consegue. Nesse sentido, vamos dividir a conservação em dois tempos, o iminente a perda de contato entre o anteparo e o bloco, e aquele em que há deformação máxima da mola, o que pode ser escrito como:\begin{matrix}
\dfrac{mv^2}{2} + mgy + \dfrac{1}{2}k(x_1)^2 = \dfrac{1}{2}k(x_2)^2
\end{matrix}Interpretando nossa equação acima, começamos por perceber que o corpo no momento de iminência apresenta velocidade $v$, o que é devidamente necessário, visto que do contrário o corpo não seria capaz de chegar em $x_2$. Por outro lado, também há energia potencial no corpo, ele está numa determinada altura $y$ e logo após isso desce até o nível de referência, este que adotamos como o ponto de deformação máxima. Além disso, há energia elástica no momento de iminência, e a deformação deve de ser simplesmente $x_1$, visto que a mola inicialmente está em seu comprimento natural. Por fim, toda energia deve ser convertida em energia elástica para deformação máxima. Certo, após toda essa análise, vamos começar encontrando $v$, basicamente, aplicando a equação de Torricelli:\begin{matrix}
v^2 = 0^2 + 2a(x_1) &\therefore& v = \sqrt{ 2a(x_1)}
\end{matrix}Encontrar $y$ também não é difícil, observe a figura abaixo:
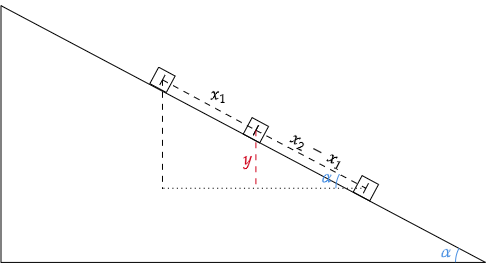 Consequentemente,\begin{matrix} y = (x_2 -x_1) \sin{\alpha}
\end{matrix}Conforme primeiro resultado obtido, encontrar $x_1$ é o menor dos problemas, assim, substituindo tudo na conservação da energia:\begin{matrix}
ma(x_1) + mg(x_2 -x_1) \sin{\alpha} + \dfrac{1}{2}k(x_1)^2 = \dfrac{1}{2}k(x_2)^2
\end{matrix}Então,\begin{matrix}
m(x_1)(a - g\sin{\alpha}) + mg(x_2)\sin{\alpha} + \dfrac{1}{2}k(x_1)^2 = \dfrac{1}{2}k(x_2)^2
\end{matrix}Substituindo $x_1$,\begin{matrix}
-m\left[\dfrac{m(g\sin{\alpha} - a)^2}{k}\right] + mg(x_2)\sin{\alpha} + \dfrac{1}{2}k\left[ \dfrac{m(g\sin{\alpha} - a)}{k}\right]^2 = \dfrac{1}{2}k(x_2)^2
\end{matrix}Veja que agora o problema se resume em resolver uma equação de segundo grau em $x_2$, podemos tentar ajeitar esta equação para:\begin{matrix}
(x_2)^2 + \dfrac{2mg \sin{\alpha}}{k}(x_2) - \dfrac{m^2(g\sin{\alpha} - a)^2}{k^2}= 0
\end{matrix}Portanto, resolvendo a equação de segundo grau:\begin{matrix}
x_2 = \dfrac{mg\sin{\alpha} + m\sqrt{a(2g\sin{\alpha} - a) }}{k}
\end{matrix}\begin{matrix}Letra \ (C)
\end{matrix}$\color{orangered}{\text{Obs:}}$ Como $x_2 > x_1$, a raiz negativa não satisfaz.
Consequentemente,\begin{matrix} y = (x_2 -x_1) \sin{\alpha}
\end{matrix}Conforme primeiro resultado obtido, encontrar $x_1$ é o menor dos problemas, assim, substituindo tudo na conservação da energia:\begin{matrix}
ma(x_1) + mg(x_2 -x_1) \sin{\alpha} + \dfrac{1}{2}k(x_1)^2 = \dfrac{1}{2}k(x_2)^2
\end{matrix}Então,\begin{matrix}
m(x_1)(a - g\sin{\alpha}) + mg(x_2)\sin{\alpha} + \dfrac{1}{2}k(x_1)^2 = \dfrac{1}{2}k(x_2)^2
\end{matrix}Substituindo $x_1$,\begin{matrix}
-m\left[\dfrac{m(g\sin{\alpha} - a)^2}{k}\right] + mg(x_2)\sin{\alpha} + \dfrac{1}{2}k\left[ \dfrac{m(g\sin{\alpha} - a)}{k}\right]^2 = \dfrac{1}{2}k(x_2)^2
\end{matrix}Veja que agora o problema se resume em resolver uma equação de segundo grau em $x_2$, podemos tentar ajeitar esta equação para:\begin{matrix}
(x_2)^2 + \dfrac{2mg \sin{\alpha}}{k}(x_2) - \dfrac{m^2(g\sin{\alpha} - a)^2}{k^2}= 0
\end{matrix}Portanto, resolvendo a equação de segundo grau:\begin{matrix}
x_2 = \dfrac{mg\sin{\alpha} + m\sqrt{a(2g\sin{\alpha} - a) }}{k}
\end{matrix}\begin{matrix}Letra \ (C)
\end{matrix}$\color{orangered}{\text{Obs:}}$ Como $x_2 > x_1$, a raiz negativa não satisfaz.

Ampliar Imagem

