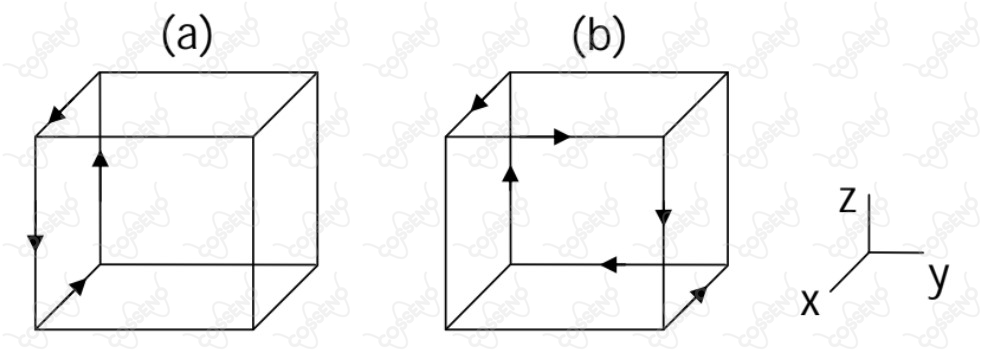
Uma corrente flui em quatro das arestas do cubo da figura (a) e produz no seu centro um campo magnético de magnitude na direção , cuja representação no sistema de coordenadas e . Considerando um outro cubo (figura (b)) pelo qual uma corrente de mesma magnitude flui através do caminho indicado, podemos armar que o campo magnético no centro desse cubo será dado por
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A princípio, note que a questão trata, basicamente, da regra da mão direita. Nesse contexto, a sutileza da questão está na análise das figuras, a ideia central é perceber que enquanto na figura $a$ a corrente flui em quatro arestas de uma mesma face, na figura $b$ a corrente flui em duas arestas de cada face. Com isso, repare que o campo magnético produzido por uma face em $b$ é metade que a face de $a$ produz, afinal, na face de $a$ flui corrente em quatro arestas, enquanto em cada face de $b$ se flui em apenas duas. Dessa forma, podemos analisar a situação em pares, veja:
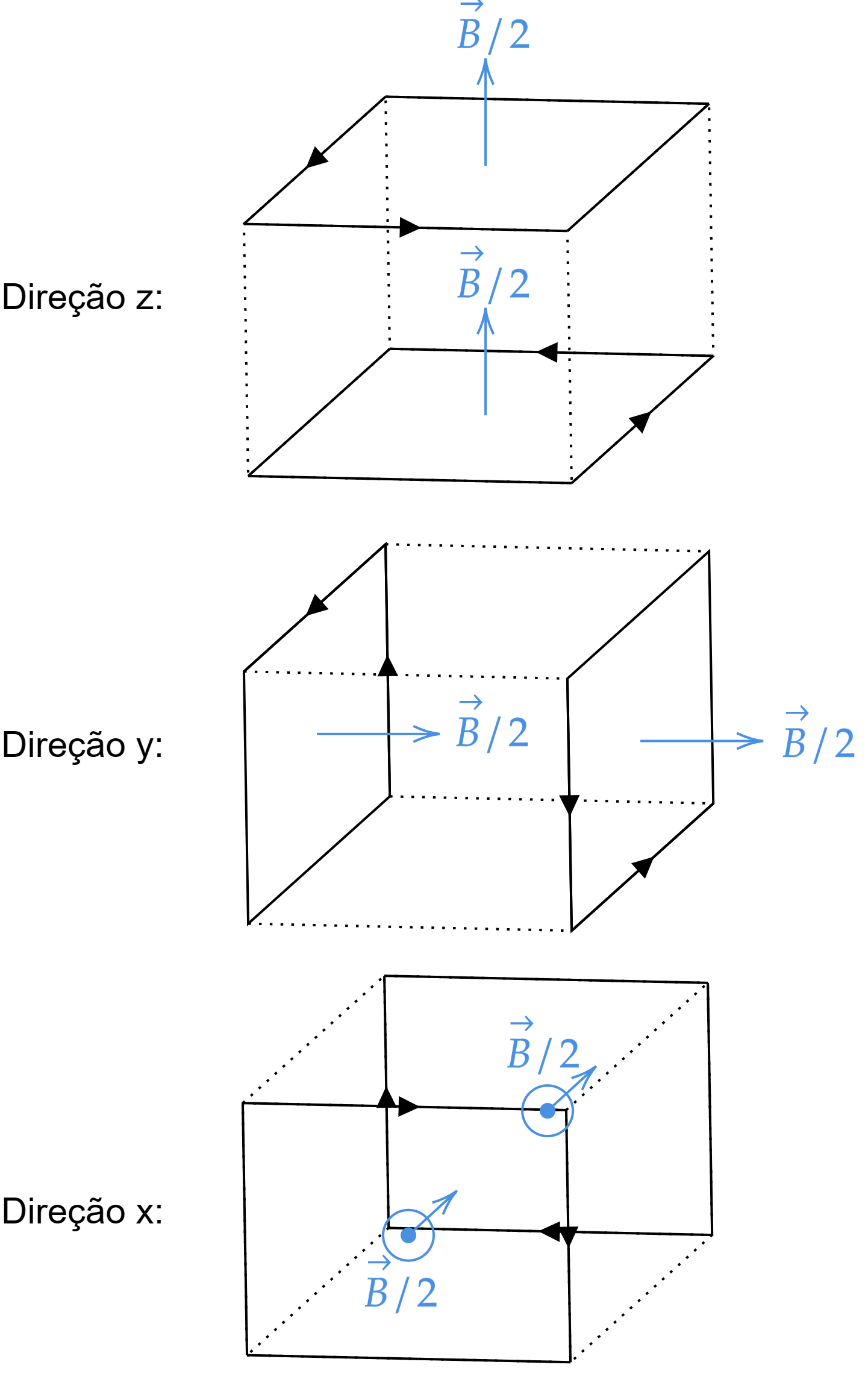 Portanto, analisando o eixo de coordenadas da figura, verificamos que em $x$ o sentido do campo é negativo, assim:\begin{matrix}\vec{B} = \vec{B}_x + \vec{B}_y + \vec{B}_z = (-B,B,B)
\end{matrix}\begin{matrix}Letra \ (B)
\end{matrix}
Portanto, analisando o eixo de coordenadas da figura, verificamos que em $x$ o sentido do campo é negativo, assim:\begin{matrix}\vec{B} = \vec{B}_x + \vec{B}_y + \vec{B}_z = (-B,B,B)
\end{matrix}\begin{matrix}Letra \ (B)
\end{matrix}

Ampliar Imagem


