A segunda lei de Kepler é derivada da conservação do momento angular, assim, caso repentinamente o efeito da gravitação deixasse de existir, o momento angular se conservaria, visto que nenhum torque externo foi aplicado ao corpo - a força gravitacional é interna ao sistema. Nesse sentido, a segunda lei de Kepler ainda é válida, isto com o corpo escapando pela tangente perfazendo um movimento retilíneo e uniforme. Além disso, é possível esboçar a situação numa análise mais simples: 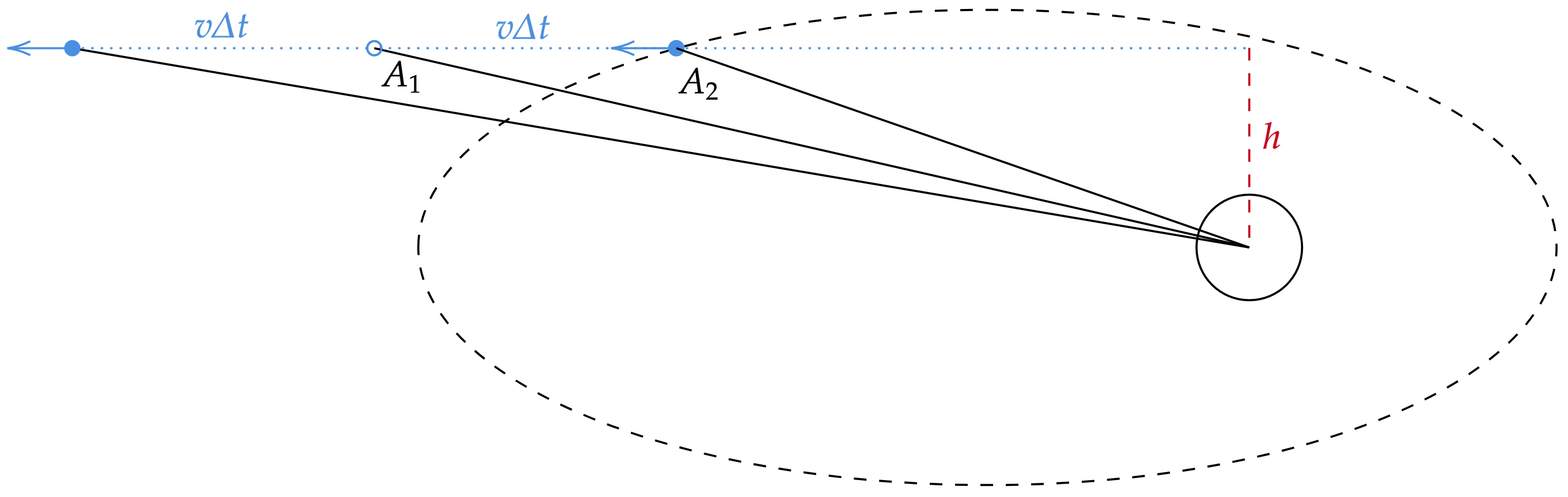Calculando as áreas em questão:\begin{matrix} A = \dfrac{base \times altura}{2} &\therefore& A_1 = A_2 = \dfrac{(v\Delta t)\times h}{2} \end{matrix}\begin{matrix}Letra \ (A) \end{matrix}