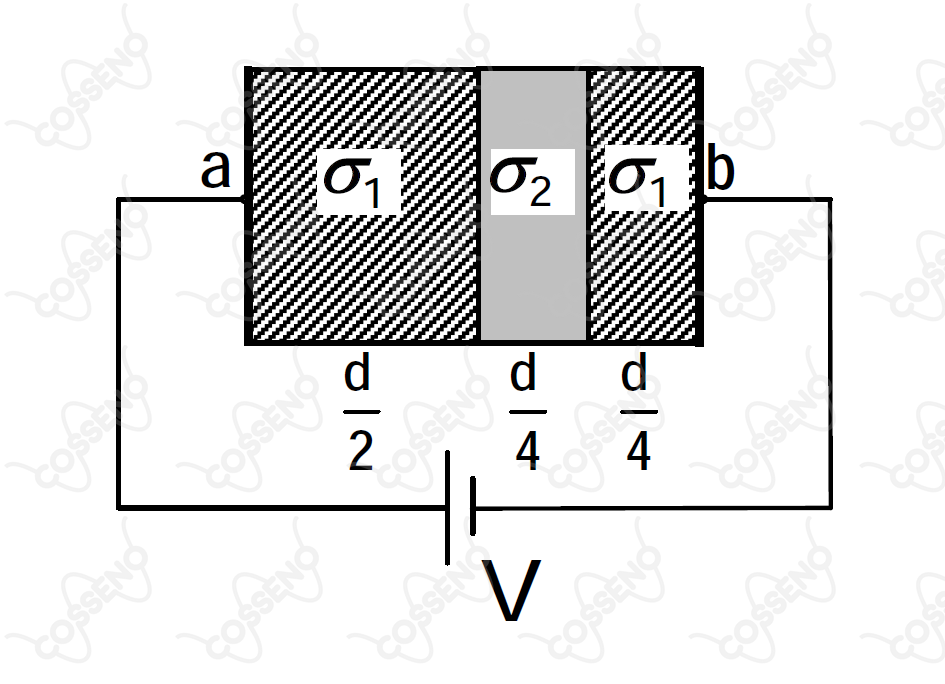
A figura mostra três camadas de dois materiais com condutividade e , respectivamente. Da esquerda para a direita, temos uma camada do material com condutividade , de largura , seguida de uma camada do material de condutividade , de largura , seguida de outra camada do primeiro material de condutividade , de largura . A área transversal é a mesma para todas as camadas é igual a . Sendo a diferença de potencial entre os pontos e igual a , a corrente do circuito é dada por
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A princípio, a questão se resume em conhecer as $\text{leis de Ohm}$ e o conhecimento básico de associação de resistores. Nesse sentido, comecemos pela segunda lei de Ohm, a qual nos permitirá encontrar a resistência das camadas, denotemos elas pelo índice $1$, $2$ e $3$, respectivamente, partindo da esquerda para direita. Com isso, têm-se:\begin{matrix}
R_1 = \dfrac{1}{\sigma_1}\cdot \dfrac{d}{2A} &,& R_2 = \dfrac{1}{\sigma_2}\cdot \dfrac{d}{4A} &,& R_3 = \dfrac{1}{\sigma_1}\cdot \dfrac{d}{4A}
\end{matrix}Realizando a associação em série dos resistores, têm-se:\begin{matrix}
R_{eq} = \dfrac{d}{4A} \left(\dfrac{3\sigma_2 + \sigma_1}{\sigma_1 \sigma_2}\right)
\end{matrix}Portanto, conforme primeira lei de Ohm:\begin{matrix}
V = R_{eq} \cdot i &\therefore& i = \dfrac{4VA(\sigma_1 \sigma_2)}{d(3\sigma_2 + \sigma_1)} \ \ \ \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}

