$• \ \text{Solução I:}$ A princípio, podemos começar esboçando a situação: 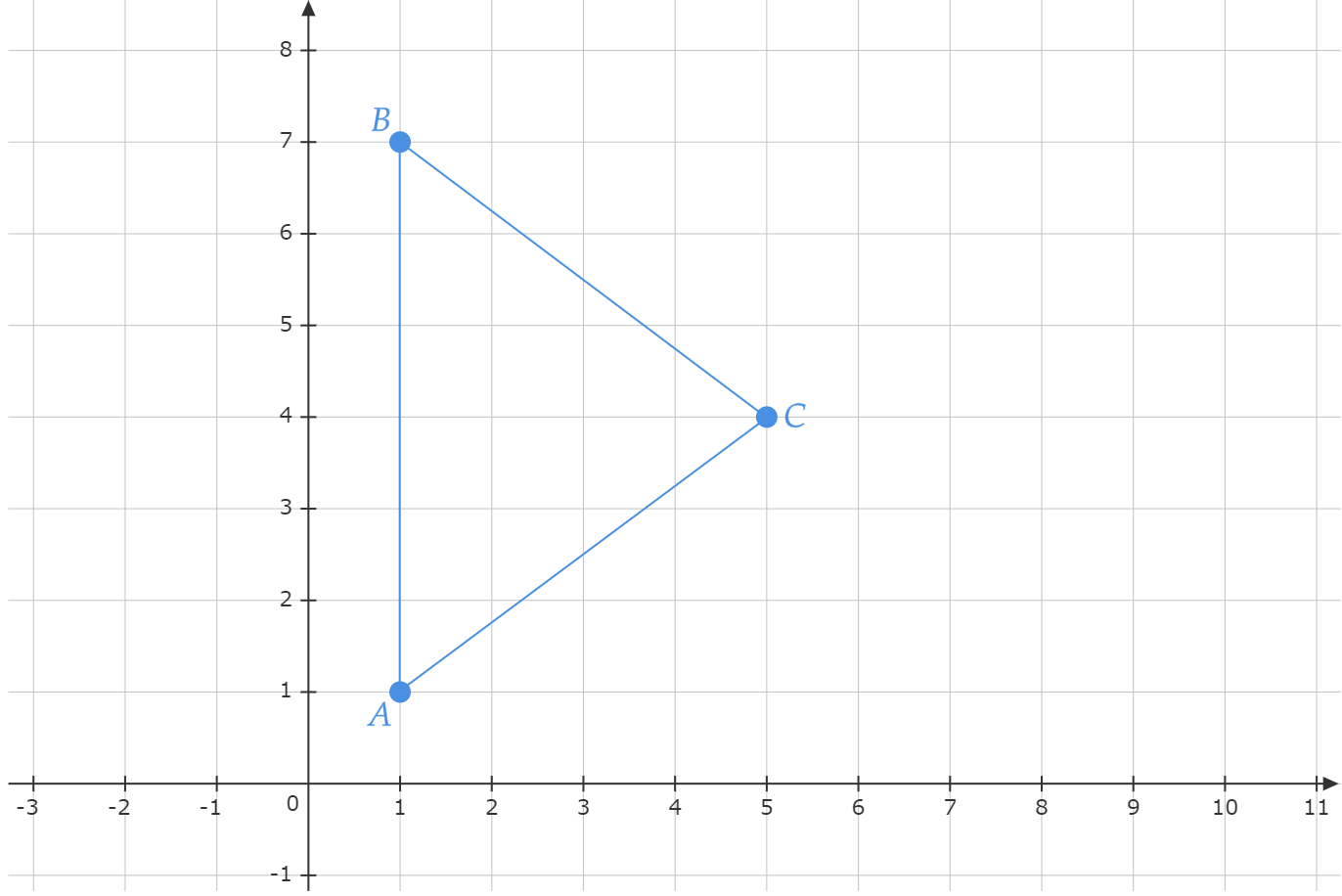Não é difícil perceber que $\overline{AB} = 6$, analogamente, aplicando a distância euclidiana (ou simplesmente Pitágoras), têm-se:\begin{matrix} (\overline{AC})^2 = (5-1)^2 + (4-1)^2 &\therefore& \overline{AC} = 5 \\ (\overline{BC})^2 = (5-1)^2 + (4-7)^2 &\therefore& \overline{BC} = 5 \end{matrix}Consequentemente, nota-se que o triângulo é isósceles, ou seja, seu incentro se encontra sobre a reta mediatriz de $\overline{AB}$. Com isso, precisamos apenas encontrar o comprimento do inraio, para isso, utilizaremos a relação:\begin{matrix} p \cdot r = [ABC] &,& p : \text{semiperímetro} \end{matrix}A área do triângulo não é um problema,\begin{matrix} [ABC] = \dfrac{6 \cdot 4}{2} = 12 \end{matrix}O semiperímetro muito menos:\begin{matrix} p = \dfrac{5+5+6}{2} = 4 \end{matrix}Então,\begin{matrix} r = \dfrac{3}{2} \end{matrix}Analisando a figura, e tendo em mente o que já foi exposto, o incentro deve se encontrar em $y_i = 4$ (sobre a mediatriz de $\overline{AB}$). Assim como em $x_i = 5/2$, pois:$$ x_i = 1 + \dfrac{3}{2} =\dfrac{ 5}{2}$$Portanto, a equação da circunferência deve ser:\begin{matrix} \left(x - \dfrac{5}{2}\right)^2 + (y - 4)^2 = \left(\dfrac{3}{2}\right)^2 \ \ \tiny{\blacksquare} \end{matrix} $• \ \text{Solução II:}$ Você também poderia partir do princípio que o incentro está na mediatriz de $\overline{AB}$ e prosseguir por outro caminho, como por exemplo, utilizar a distância entre um ponto e uma reta. No caso, seria necessário saber que a distância do incentro aos lados do triângulo apresenta mesma medida $r$. Assim, relacionando as distâncias entre as retas e o centro, soluciona-se o problema. Nesse contexto, comecemos encontrando uma reta, partindo do coeficiente angular de $AC$:\begin{matrix} m_{AC} = \dfrac{4-1}{5-1} = \dfrac{3}{4} \end{matrix}Então a reta $AC$ é dada pela equação:\begin{matrix}3x - 4y + 1 = 0 \end{matrix}O incentro se encontra em $(x_i,4)$, tal que o inraio $r = |x_i -1|$, ou seja:\begin{matrix} r = \dfrac{|3x_i - 4\cdot 4 + 1|}{\sqrt{3^2 + 4^2}} = |x_i - 1| \end{matrix}Resolvendo a equação acima, encontra-se dois resultados, o negativo não nos interessa pois $x_i > 0$, logo:\begin{matrix} x_i = \dfrac{5}{2} &\therefore& r = \dfrac{3}{2} \end{matrix}E assim segue o resultado análogo ao da solução anterior. $• \ \text{Solução III:}$ Um meio mais "analítico" e até pragmático de se resolver seria conhecer a equação analítica do incentro, que nesse caso pode ser dada como:\begin{matrix} (x_i,y_i) = \dfrac{(x_C,y_C)\overline{AB} + (x_B,y_B)\overline{AC} + (x_A,y_A)\overline{BC}}{\overline{AB} + \overline{AC} + \overline{BC}} \end{matrix}Veja que seria necessário apenas encontrar o comprimento dos lados para encontrar o incentro, o que já fizemos a partir do conhecimento da distância euclidiana. Desse modo, substituindo os resultado, têm-se:\begin{matrix} x_i = \dfrac{5}{2} &\wedge& y_i = 4 \end{matrix}Nesse momento, seria necessário encontrar o inraio, o que pode ser feito de diversas maneiras. Seja pela equação de área como na primeira solução, ou a análise do gráfico e distância entre ponto e reta como na segunda. Conduto, existe outra forma, diga-se de passagem, que requer menos conhecimento do que as demais (mas bem mais trabalho). Por exemplo, vamos supor que você não soubesse que o incentro se encontra sobre a mediatriz de $\overline{AB}$, mas você sabe que o inraio é perpendicular ao lado do triângulo. Ora, há de se perceber que ao ligar dois pontos ao incentro, forma-se outro triângulo, e o inraio deve de ser sua altura. Pensando em dois pois, podemos pegar $A$ e $B$, tal que temos o triângulo $ABI$, com $I$ sendo o incentro. Novamente, aplicando a distância euclidiana, constata-se:\begin{matrix} (\overline{AI})^2 = \left(\dfrac{5}{2} - 1\right)^2 + (4-1)^2 &\therefore& \overline{AI} = \dfrac{3\sqrt{5}}{2} \\ (\overline{BI})^2 = \left(\dfrac{5}{2} - 1\right)^2 + (4-7)^2 &\therefore& \overline{BI} = \dfrac{3\sqrt{5}}{2} \end{matrix}Perceba que o triângulo $ABI$ também é isósceles, ou seja, por Pitágoras, têm-se:\begin{matrix} r^2 = \left(\dfrac{3\sqrt{5}}{2} \right)^2 - \left(\dfrac{\overline{AB}}{2}\right)^2 &\therefore& r = \dfrac{3}{2} \end{matrix}E assim, novamente segue o resultado.