$• \ \text{Afirmativa I:}$ $\color{#3368b8}{\text{Verdadeira}}$ Dizer que $x \in A \cap B$ significa que existe um elemento $x$ presente concomitantemente no conjunto $A$ e $B$. Nesse sentido, queremos negar essa simultaneidade, o que é suficiente dizer que $x$ não pertence a $A$ ou $B$. $• \ \text{Afirmativa II:}$ $\color{#3368b8}{\text{Verdadeira}}$ Esta é basicamente a aplicação de uma das $\text{propriedades distributivas dos conjuntos}$. Todavia, caso você não lembrasse dela, seria possível simplesmente desenhar os $\text{Diagramas de Euler-Venn}$ e verificar: 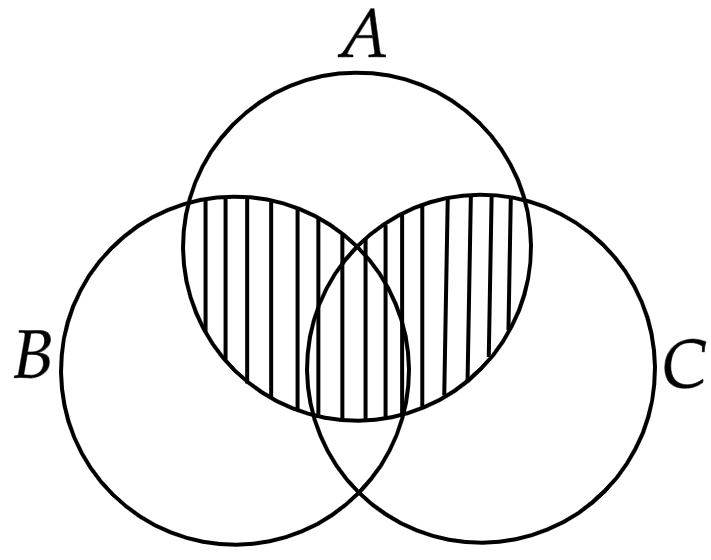$• \ \text{Afirmativa III:}$ $\color{#3368b8}{\text{Verdadeira}}$ Esta é basicamente $\text{diferença simétrica}$ $A\Delta B$, que também poderia ser verificada pelos $\text{Diagramas de Euler-Venn}$: 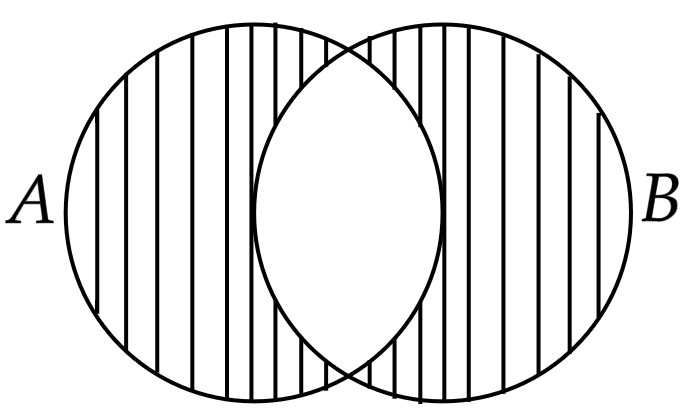\begin{matrix}Letra \ (E) \end{matrix}