A princípio, podemos começar esboçando a situação, segundo enunciado, o cilindro está inscrito no tetraedro, isto nos confere que sua face superior deve tangenciar as faces laterais do tetraedro. (Atente que isso não confere que a base do cilindro também tangencie as faces laterais.) Nesse sentido, temos: 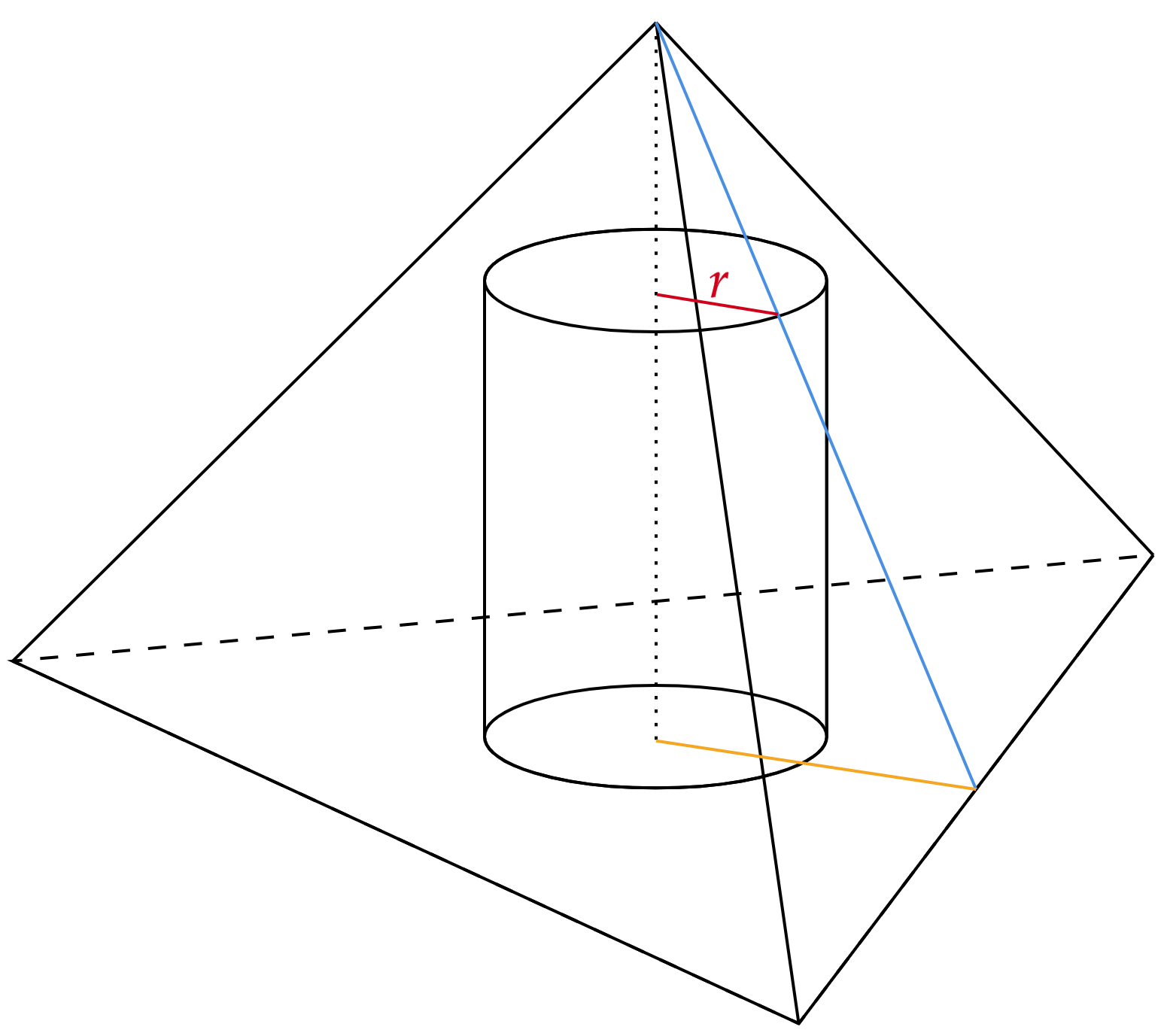Planificando o triângulo composto pela altura $H$ do tetraedro, a altura $y$ da face, têm-se: 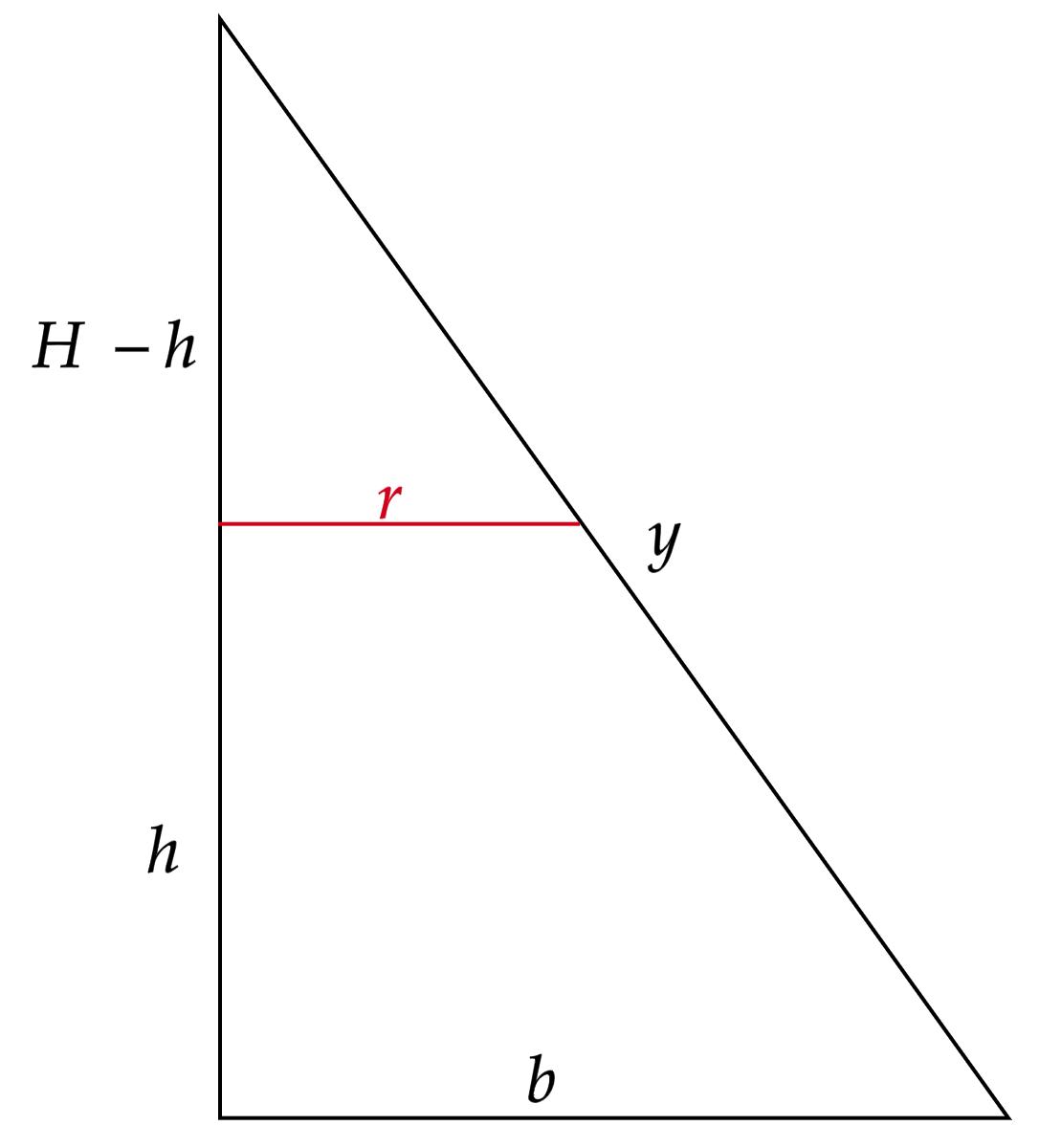Observe que por uma simples semelhança de triângulos conseguimos relacionar alguns temos da imagem:\begin{matrix} \dfrac{r}{H-h} = \dfrac{b}{H} \end{matrix}Conforme enunciado, já conhecemos $h$, agora nos resta encontrar $r$ a fim de verificar o volume do cilindro. Para isso, antes precisamos encontrar $b$, e $H$, comecemos por $H$: 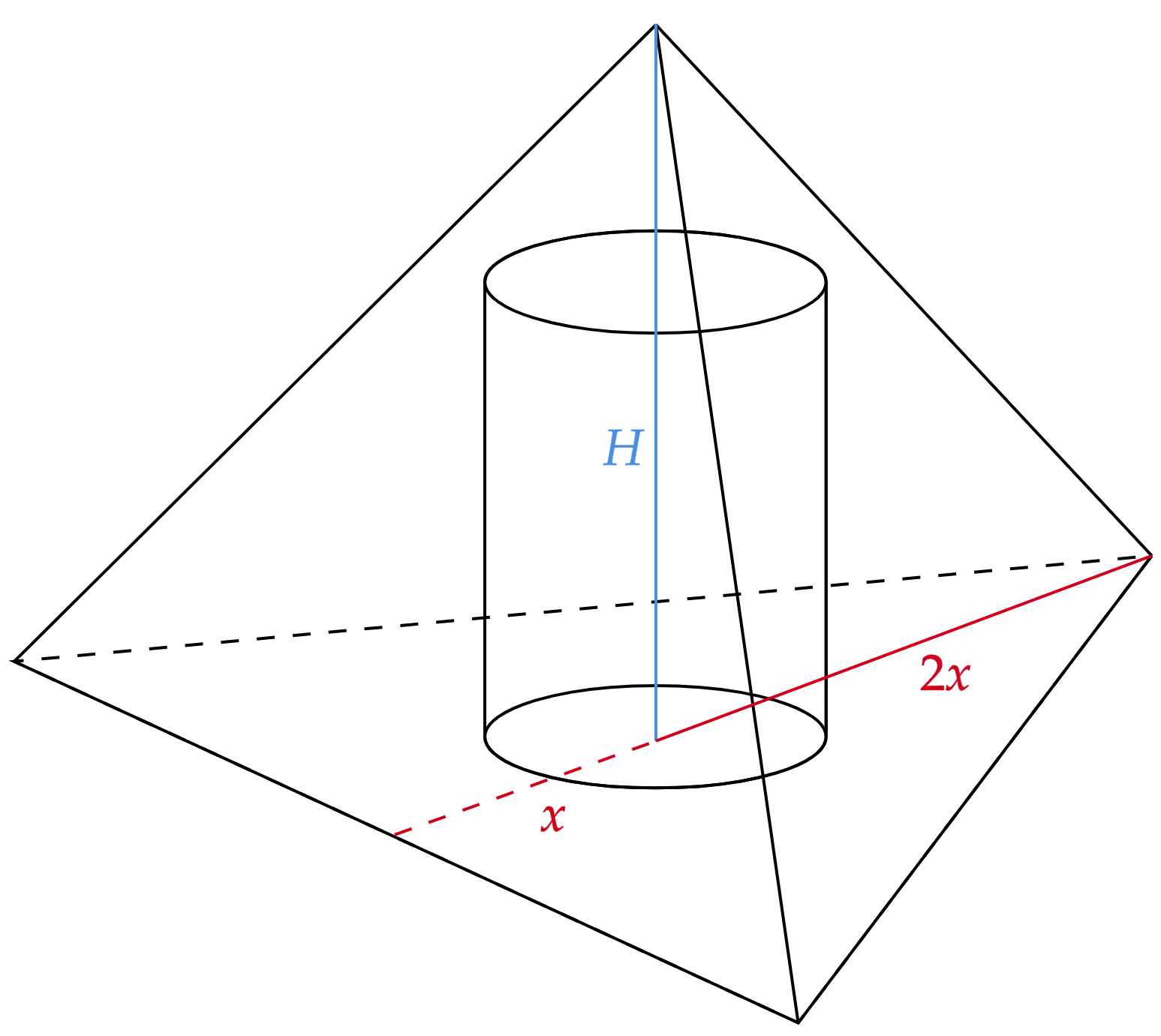Primeiro, com conhecimento das propriedades do baricentro, pela altura do triângulo da base:\begin{matrix} 3x = \dfrac{3\sqrt{3}}{2} &\therefore& 2x = \sqrt{3} \end{matrix}Conforme teorema de Pitágoras:\begin{matrix} 3^2 = (2x)^2 + H^2 &\therefore& H = \sqrt{6} \end{matrix}$\color{orangered}{\text{Obs:}}$ Seria interessante você já ter de cabeça o resultado da altura de um tetraedro regular, que é $\dfrac{l\sqrt{6}}{3}$, em que $l$ é a aresta do tetraedro. Uma incógnita já foi resolvida, agora vamos pensar em $b$, pela segundo imagem, novamente, pelo teorema de Pitágoras:\begin{matrix} y^2 = b^2 + H^2 \end{matrix}Encontrar $y$ não é difícil, é simplesmente a altura do triângulo da face, ou seja:\begin{matrix} y = \dfrac{3\sqrt{3}}{2} &\Rightarrow& b = \dfrac{\sqrt{3}}{2} \end{matrix}Agora, já é possível encontrar $r$, veja:\begin{matrix} \dfrac{r}{\sqrt{6}-\dfrac{\sqrt{6}}{3}} = \dfrac{\dfrac{\sqrt{3}}{2}}{\sqrt{6}} &\therefore& r = \dfrac{\sqrt{3}}{3} \end{matrix}Por fim, o volume $V$ do cilindro:\begin{matrix} V = (\pi r^2)h &\therefore& V = \dfrac{\pi \sqrt{6}}{9} \ \ \tiny{\blacksquare} \end{matrix}\begin{matrix}Letra \ (D) \end{matrix}

$\text{Observações Iniciais:}$ - Fórmula da área de um triângulo equilátero: $\dfrac{a^2\cdot \sqrt{3}}{4}$, sendo $a$ a medida do lado; - Fórmula da altura de um tetraedro regular: $\dfrac{a\cdot \sqrt{6}}{3}$, sendo $a$ a medida da aresta; - Fórmula da área $A$ de um triângulo, em função do raio $r$ da circunferência inscrita: $A = pr$, em que $p$ é o semi-perímetro do triângulo. - chamarei de $h_c = \dfrac{\sqrt{6}}{3}$ a altura do cilindro. Imaginemos um plano paralelo à base do tetraedro, que contém a base superior do cilindro e, portanto, divide o tetraedro original em dois tetraedros semelhantes, o maior e original, de altura $h_1 = 3\cdot \dfrac{\sqrt{6}}{3} = \sqrt{6}$ e área da base $\dfrac{9\sqrt{3}}{4}$ (vide $\text{Observações~Iniciais}$), e o menor, de altura $h_2 = h_1-h_{c} = \dfrac{2\sqrt{6}}{3}$ e área da base que chamarei de $b$. Pelas relações de semelhança, temos:$$\dfrac{b}{\frac{9\sqrt{3}}{4}} = \left(\dfrac{\frac{2\sqrt{6}}{3}}{\sqrt{6}}\right)^2 \implies \dfrac{4}{9}\cdot \dfrac{b}{\sqrt{3}} = \dfrac{4}{9} \implies b = \sqrt{3} = \dfrac{a^2\cdot \sqrt{3}}{4} \implies a = 2$$Descobre-se acima que a área da base triangular do tetraedro menor é $\sqrt{3}$ e, assim, o seu lado mede $2$. Com isso, é possível determinar o raio da base do cilindro, como se segue abaixo:$$b = pr \implies \sqrt{3} = \dfrac{2+2+2}{2}\cdot r \implies r = \dfrac{\sqrt{3}}{3}$$Portanto, o volume $V$ do cilindro é$$V = \pi r^2h = \pi \cdot\dfrac{1}{3}\cdot \dfrac{\sqrt{6}}{3} \implies \boxed{V = \dfrac{\pi\sqrt{6}}{9}}$$$$\bf{Alternativa~(D)}$$