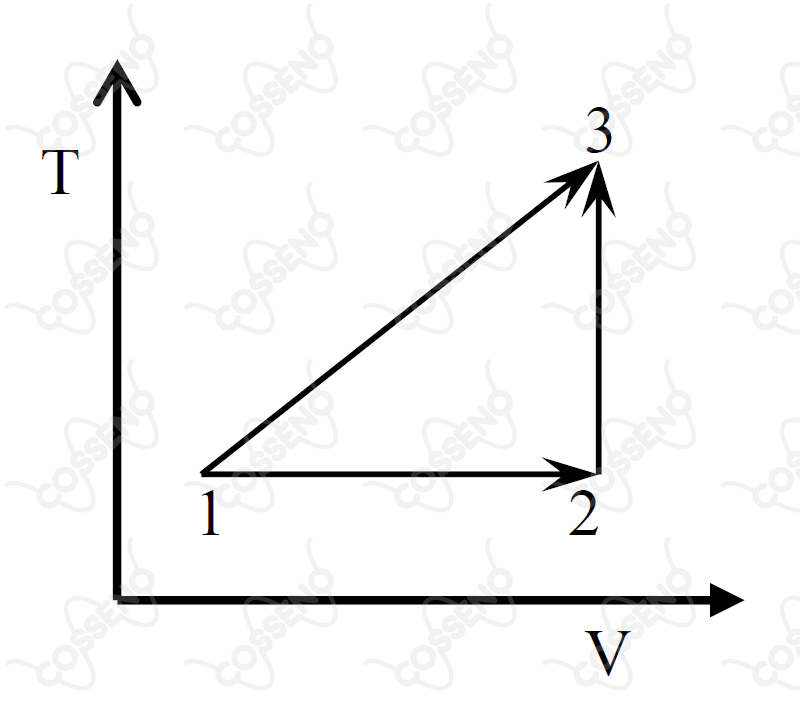
O diagrama temperatura () versus volume () representa hipoteticamente as transformações pelas quais um gás ideal no estado pode atingir o estado . Sendo a variação de energia interna e a quantidade de calor trocado com a vizinhança, assinale a opção com a afirmação ERRADA em relação às transformações termodinâmicas representadas no diagrama.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$• \ \text{Alternativa (A):}$ $\color{orangered}{\text{Errada}}$
O processo é uma expansão isotérmica, assim, conforme a primeira lei da termodinâmica, para um gás ideal: $\Delta U_{12} = 0$, tal que:\begin{matrix} \Delta U_{12} = Q_{12} - W_{12}
\end{matrix}Como $W_{12} \ne 0$, então $Q_{12} \ne 0$.
$• \ \text{Alternativa (B):}$ $\color{#3368b8}{\text{Correta}}$
A energia interna é uma função de estado, assim, visto os estágios iniciais e finais, sabemos que a variação de temperatura é a mesma nos dois processos. Com isso, conforme um gás ideal, a variação de energia interna deve ser a mesma, já que:\begin{matrix}
\Delta U = \dfrac{f}{2}nR\Delta T &\therefore& |\Delta U_{13}| = |\Delta U_{23}|
\end{matrix}$• \ \text{Alternativa (C):}$ $\color{#3368b8}{\text{Correta}}$
Analisando o gráfico, facilmente notamos que o processo é isocórico, o que corrobora o resultado da alternativa.
$• \ \text{Alternativa (D):}$ $\color{#3368b8}{\text{Correta}}$
O processo de $2$ para $3$ é uma expansão isocórica, ou seja, $\Delta U_{23} >0$. Analogamente, já sabemos que $\Delta U_{12} = 0$, ou seja, o resultado segue.
$• \ \text{Alternativa (E):}$ $\color{#3368b8}{\text{Correta}}$
Conforme análise anterior, $\Delta U_{23} >0$, consequentemente, $Q_{23} >0$, visto que o processo é isocórico, isto é, $W_{23} =0$.\begin{matrix} Letra \ (A)
\end{matrix}

