A princípio, observe as alternativas, nenhuma delas conta com o arco ao qual pertence o ângulo em análise, logo, é de admitir que o ângulo é pequeno, pois assim teríamos:\begin{matrix}\tan{\theta} \approx \sin{\theta} \approx \theta \end{matrix}Com isso, vamos esboçar a situação, 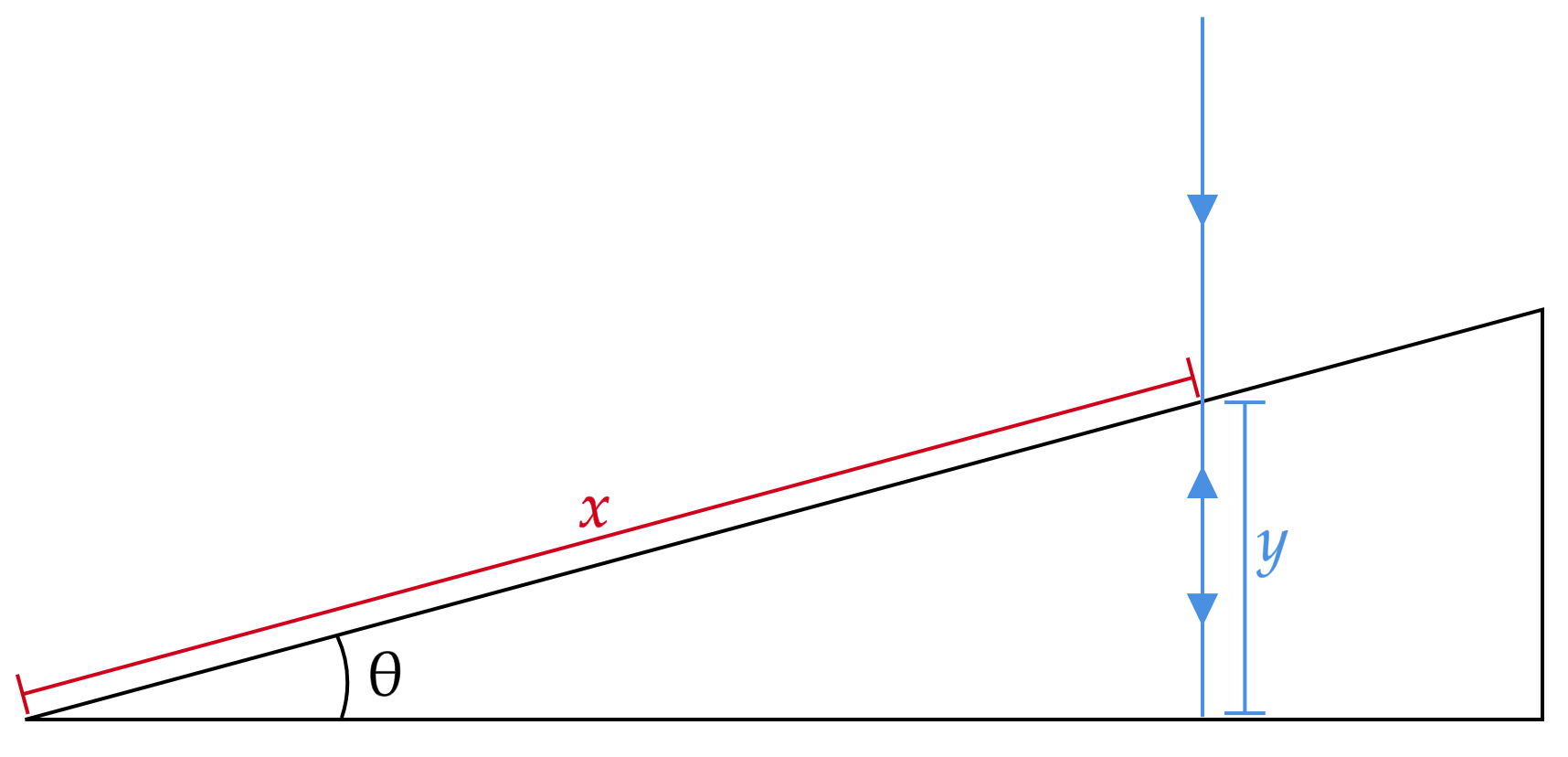Primeiramente, vale ressaltar que a figura apresenta dimensões grotescas, mas tente imaginar a situação para um ângulo pequeno, a refração será mínima, aproximando-se da linearidade da figura. Nessa perspectiva, podemos começar com:\begin{matrix} \theta = \dfrac{y}{x} &\because& \sin{\theta} \approx \dfrac{y}{x} \end{matrix}Pensando em $x$, a partir do enunciado, constata-se:\begin{matrix} x = m \cdot \dfrac{e}{2} \end{matrix}$\color{orangered}{\text{Obs:}}$ Pondere que para cada distância $e$ se corresponde duas franjas escuras, ou seja, para $m$ franjas, deve-se percorrer o resultado acima. Além disso, pensando na diferença de caminho óptico:\begin{matrix}2y = m\dfrac{\lambda_{vidro}}{2} &\therefore&y = m\dfrac{\lambda_{vidro}}{4} \end{matrix}Então, já temos:\begin{matrix} \theta = \dfrac{\lambda_{vidro}}{2e} \end{matrix}Pondere que as respostas não estão em $\lambda_{vidro}$, mas sim em $\lambda$. Nessa perspectiva, utilizando a lei de Snell-Descartes,\begin{matrix} \dfrac{\lambda_{vidro}}{\lambda} = \dfrac{n_{ar}}{n} &,& n_{ar} := 1 \end{matrix}Portanto:\begin{matrix}\boxed{\theta = \dfrac{\lambda}{2ne} } \end{matrix}\begin{matrix}Letra \ (A) \end{matrix}