Assumindo que as dimensões das bolas são desprezíveis conforme omissão, podemos dividir a situação em dois momentos: uma imediatamente antes da colisão, e outro imediatamente depois. Com isso, podemos esboçar a situação: 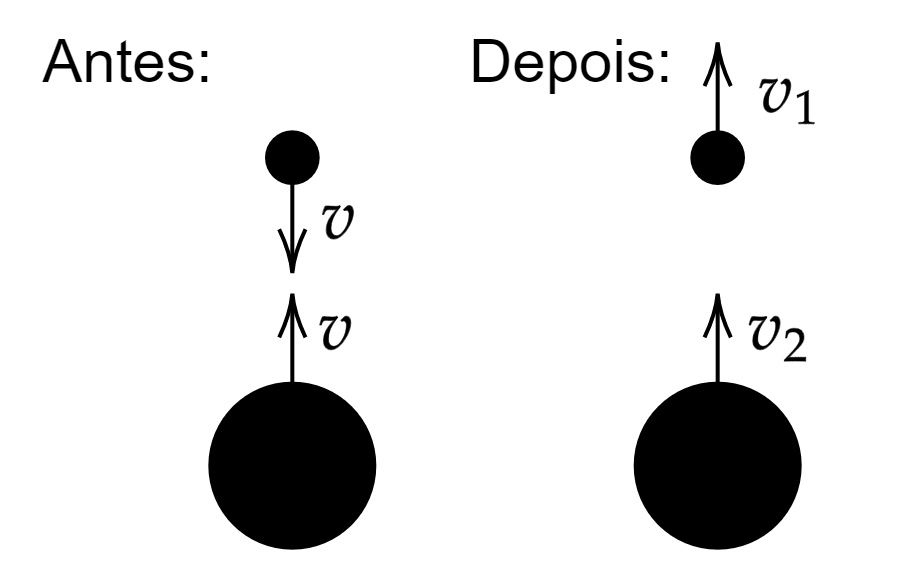$\color{orangered}{\text{Obs:}}$ O esboço é grosseiro, mas não se esqueça que ambas as dimensões são desprezíveis, por isso, imediatamente antes da colisão ambas as bolas apresentam mesma velocidade, afinal, ambas caíram a partir do repouso e percorreram a mesma distância. Além disso, veja que a colisão da bola de basquete com o chão foi omitida, visto que as colisões são perfeitamente elásticas, ou seja, há completa conservação da energia cinética. Realizando a conservação do momento linear antes e após a colisão, admitindo o sentido para cima como positivo, têm-se:\begin{align} 600v - 60v &=600v_2 +60v_1 \\ 9v &=10v_2 + v_1 \end{align}Pensando agora na colisão,\begin{matrix} e = \dfrac{v_1 - v_2}{v + v} &,& e =1 &\therefore&v_2 = v_1 - 2v \end{matrix}Relacionando os dois resultados computados,\begin{matrix}v_1 = \dfrac{29}{11} v \end{matrix}Encontrar $v$ não é difícil, basta aplicar a equação de Torricelli:\begin{matrix} v^2 = 0^2 + 2(10)(5) &\Rightarrow& v = 10 \ \pu{m/s} &\therefore& v_1 = \dfrac{290}{11} \ \pu{m/s} \end{matrix}Novamente, aplicando Torricelli, pode-se encontrar a máxima altura $d$ alcançada pela bola de tênis:\begin{matrix} 0^2 = v_1^2 + 2(-10)d &\therefore&\boxed{ d \approx 35 \ \pu{m}}\end{matrix}\begin{matrix}Letra \ (E) \end{matrix}