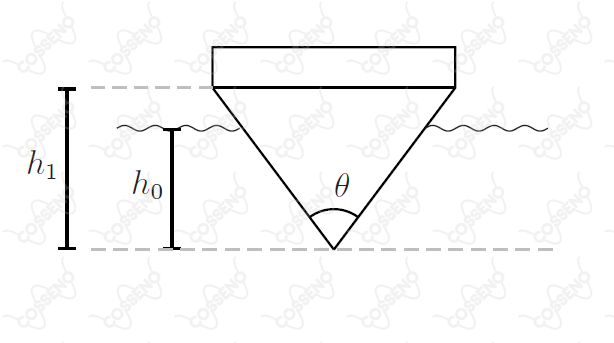
Uma balsa tem o formato de um prisma reto de comprimento e seção transversal como vista na figura. Quando sem carga, ela submerge parcialmente até a uma profundidade . Sendo a massa específica da água e a aceleração da gravidade, e supondo seja mantido o equilíbrio hidrostático, assinale a carga que a balsa suporta quando submersa a uma profundidade .
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Seja $M$ a massa da balsa , $b$ a base da balsa , $V_{1}$ o volume submerso da balsa na situação $1$ e $V_{2}$ o volume submerso da balsa na situação $2$.
Situação $1$ : Análise do equilíbrio da balsa sem suportar a carga $P$ :
As forças atuantes na balsa é o seu peso $Mg$ e a força de empuxo $\rho \cdot V_{1} \cdot g$. Podemos escrever que :
$Mg =\rho \cdot V_{1} \cdot g $
Situação $2$ : Análise do equilíbrio da balsa suportando a carga $P$ :
As forças atuantes na balsa é o seu peso $Mg$ , o peso $P$ da carga e a força de empuxo $\rho \cdot V_{2} \cdot g$. Dado o equilíbrio podemos escrever que:
$Mg + P = \rho \cdot V_{2} \cdot g \implies P = \rho \cdot V_{2} \cdot g - \rho \cdot V_{1} \cdot g$
$\implies P = \rho g (V_{2} - V_{1})$
Cálculo de $V_{2}:$
$V_{2} = \dfrac{b \cdot h_{1}}{2} \cdot L$
Note que $\tan \left(\dfrac{\theta}{2}\right) = \dfrac{\dfrac{b}{2}}{h_{1}} \implies \dfrac{b}{2} =\tan \left(\dfrac{\theta}{2}\right) \cdot h_{1} $
$\therefore$
$V_{2} = \dfrac{b \cdot h_{1}}{2} \cdot L = \tan \left(\dfrac{\theta}{2}\right) \cdot h_{1} \cdot h_{1} \cdot L = V_{2} = \tan \left(\dfrac{\theta}{2}\right) \cdot h_{1}^2 \cdot L $
Calculando $V_{1}$ de forma similar ao cálculo de $V_{2}$ , podemos encontrar que :
$V_{1} = \tan \left(\dfrac{\theta}{2}\right) \cdot h_{0}^2 \cdot L $
$\therefore$
$P = \rho g (V_{2} - V_{1}) = \rho g \left( \tan \left(\dfrac{\theta}{2}\right) \cdot h_{1}^2 \cdot L -\tan \left(\dfrac{\theta}{2}\right) \cdot h_{0}^2 \cdot L \right)$
$= \boxed{P = \rho g L(h_{1}^2 - h_{0}^2)\tan \left(\dfrac{\theta}{2}\right)}$
$\textbf{Resposta : Alternativa D}$
Analisando a situação inicial, isto é, a situação em que o equilíbrio reside apenas no empuxo relativo ao peso da balsa, têm-se:\begin{align} P_{balsa} &= E_{inicial} \\ P_{balsa} &= \rho g V_{inicial}
\end{align}Encontrar $V_{inicial}$ não é difícil, observe a imagem, nela, facilmente identificamos um triângulo isósceles de altura variável. (A variação da altura é relativa à imersão do prisma, o que nos interessa é o corpo imerso.) Nesse sentido, precisamos da área deste triângulo, então, vejamos:
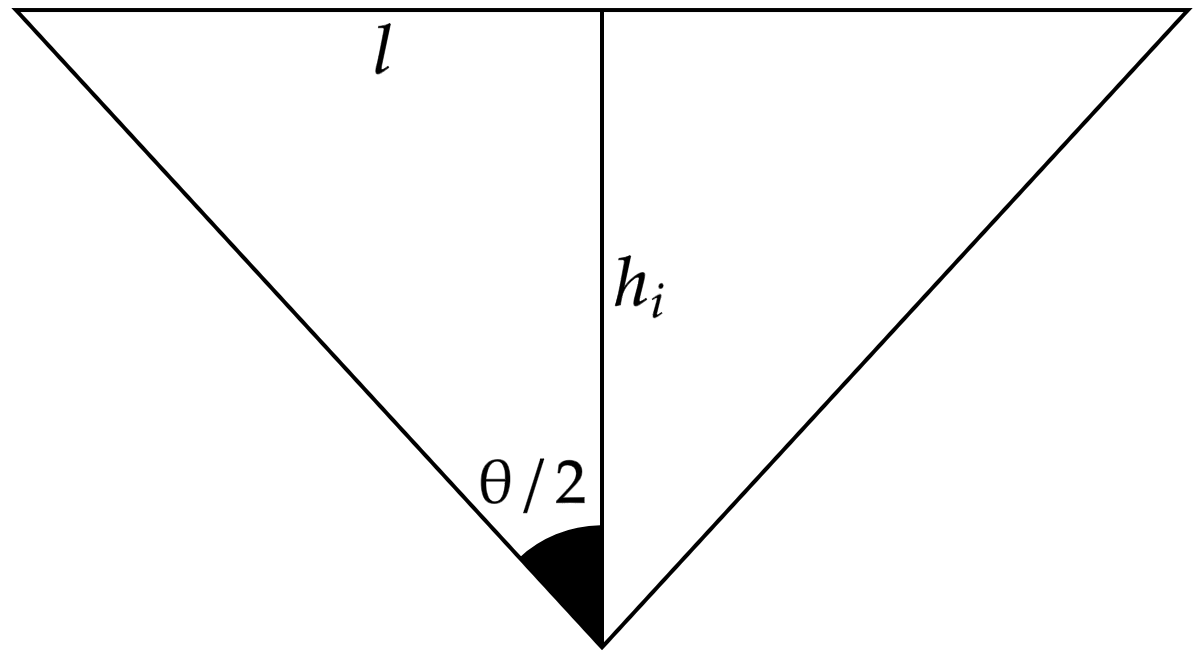 Consequentemente:\begin{matrix}
\tan{\left(\dfrac{\theta}{2} \right)} = \dfrac{l}{h_i} &\therefore& l = h_i \cdot \tan{\left(\dfrac{\theta}{2} \right)}
\end{matrix}Então a área $\Delta$ do triângulo é:\begin{matrix}
\Delta = 2\left(\dfrac{h_i \cdot l}{2}\right) =(h_i)^2 \cdot \tan{\left(\dfrac{\theta}{2} \right)}
\end{matrix}Com isso, $V_{inicial}$ é:\begin{matrix}
V_{inicial} = L \cdot \Delta_{inicial} &\therefore& V_{inicial} = L \cdot (h_0)^2 \cdot \tan{\left(\dfrac{\theta}{2} \right)}
\end{matrix}Portanto, o peso da balsa é:\begin{matrix}P_{balsa} = \rho g L (h_0)^2 \tan{\left(\dfrac{\theta}{2} \right)}
\end{matrix}Agora, para situação final, isto é, aquela que se acresce um peso $P$, têm-se o novo equilíbrio:\begin{matrix} P_{balsa} + P = E_{final}
\end{matrix}\begin{matrix} P = \rho g L (h_1)^2 \tan{\left(\dfrac{\theta}{2} \right)} - \rho g L (h_0)^2 \tan{\left(\dfrac{\theta}{2} \right)}
\end{matrix}\begin{matrix}\boxed{P = \rho g L ( h^2_1 - h^2_0) \tan{\left(\dfrac{\theta}{2} \right)}}
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}
Consequentemente:\begin{matrix}
\tan{\left(\dfrac{\theta}{2} \right)} = \dfrac{l}{h_i} &\therefore& l = h_i \cdot \tan{\left(\dfrac{\theta}{2} \right)}
\end{matrix}Então a área $\Delta$ do triângulo é:\begin{matrix}
\Delta = 2\left(\dfrac{h_i \cdot l}{2}\right) =(h_i)^2 \cdot \tan{\left(\dfrac{\theta}{2} \right)}
\end{matrix}Com isso, $V_{inicial}$ é:\begin{matrix}
V_{inicial} = L \cdot \Delta_{inicial} &\therefore& V_{inicial} = L \cdot (h_0)^2 \cdot \tan{\left(\dfrac{\theta}{2} \right)}
\end{matrix}Portanto, o peso da balsa é:\begin{matrix}P_{balsa} = \rho g L (h_0)^2 \tan{\left(\dfrac{\theta}{2} \right)}
\end{matrix}Agora, para situação final, isto é, aquela que se acresce um peso $P$, têm-se o novo equilíbrio:\begin{matrix} P_{balsa} + P = E_{final}
\end{matrix}\begin{matrix} P = \rho g L (h_1)^2 \tan{\left(\dfrac{\theta}{2} \right)} - \rho g L (h_0)^2 \tan{\left(\dfrac{\theta}{2} \right)}
\end{matrix}\begin{matrix}\boxed{P = \rho g L ( h^2_1 - h^2_0) \tan{\left(\dfrac{\theta}{2} \right)}}
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}

Ampliar Imagem


