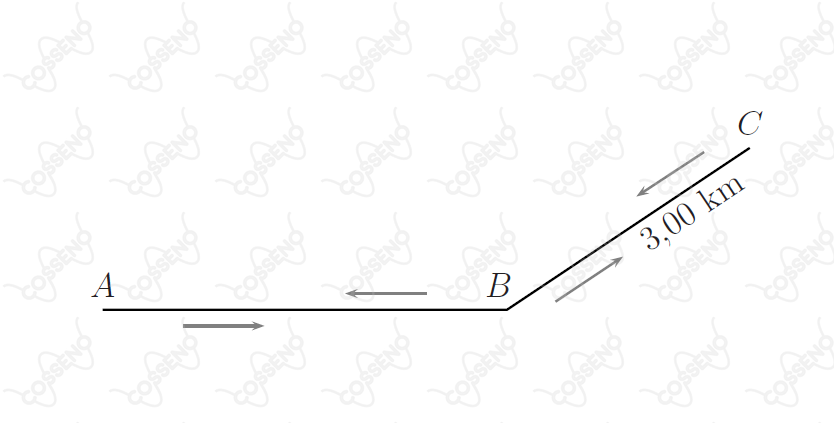
Na figura, um ciclista percorre o trecho com velocidade escalar média de e, em seguida, o trecho de de extensão. No retorno, ao passar em , verifica ser de sua velocidade escalar média no percurso então percorrido, . Finalmente, ele chega em perfazendo todo o percurso de ida e volta em , com velocidade escalar média de . Assinale o módulo do vetor velocidade média referente ao percurso .
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A princípio, vamos partir do segundo e terceiro períodos do enunciado. A partir do terceiro, pode-se encontrar a distância $\overline{AB}$, adiante, conforme segundo período, consegue-se encontrar o período de deslocamento $ABCB$, veja:\begin{matrix}
\overline{AB} + 2(3) = 20 \cdot t_{ABCB} &,& 2(\overline{AB} + 3) = 24 \cdot t_{ABCBA}
\end{matrix}$\color{orangered}{\text{Obs:}}$ $t_{ABCBA} = 1 \ \pu{h}$
Relacionando os resultados, constatamos:\begin{matrix} \overline{AB} = 9 \ \pu{km} &,& t_{ABCB} = \dfrac{3}{4} \ \pu{h}
\end{matrix}Agora, queremos o módulo $v$ do vetor velocidade média referente ao percurso $ABCB$, ou seja:\begin{matrix}
v = \dfrac{x_B - x_A}{t_{ABCB}} &,& \overline{AB} = x_B - x_A
\end{matrix}Portanto,\begin{matrix} \boxed{v = 12,0 \ \pu{km/h}}
\end{matrix}\begin{matrix}Letra \ (A)
\end{matrix}$\color{}{\text{Comentário:}}$ A letra $B$ não é válida pois não respeita os algarismos significativos impostos pelo enunciado. (É tranquilo dizer isso pois todos os dados compreendem três algarismos significativos.) No caso, isso tem a ver com margem de precisão, a letra $A$ nos diz que a velocidade está entre $12,5 \ \pu{km/h}$ e $11,5 \ \pu{km/h}$. Enquanto a letra $B$ nos diz $12,05 \ \pu{km/h}$ e $11,55 \ \pu{km/h}$.

