A princípio, vamos tentar lidar com o problema pensando em coordenadas cartesianas, pois ao encontrar os pontos que correspondem as posições dos corpos, facilmente descobrimos a distância eles pela distância euclidiana. Nesse sentido, vamos esboçar a situação para ficar mais claro: 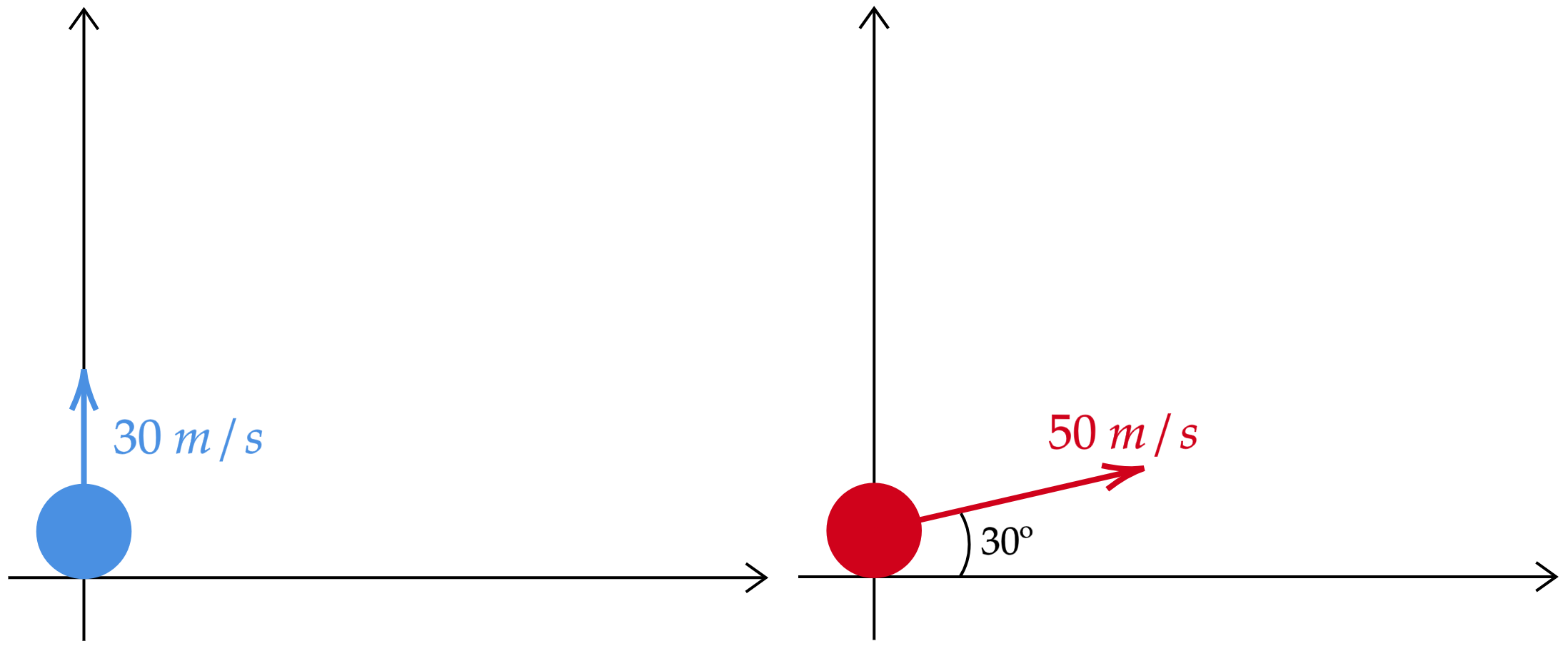$\text{Bola I:}$ Com isso, vamos começar encontrando a o instante em que a primeira bola alcança sua máxima altura, assim como sua posição no plano cartesiano nesse instante. Assim, com conhecimento das equações horárias:\begin{matrix} v_{f} = v_{i} + (-g)\Delta t &,& v_f = 0 &\therefore& \Delta t = 3 \ \pu{s} \end{matrix}$\color{orangered}{\text{Obs:}}$ Estamos assumindo o sentido positivo para cima e voltado para direita. Constatado o tempo, facilmente podemos encontrar a posição vertical, veja:\begin{matrix} y_f - y_i = v_f \Delta t - (-g)\dfrac{(\Delta t)^2}{2} &,& y_i = 0 \end{matrix}Então,\begin{matrix}y_f = 45 \ \pu{m} \end{matrix}Portanto, no plano cartesiano, a posição da bola é: $ (0 , 45)$ $\text{Bola II:}$ Agora, reta-nos analisar o lançamento oblíquo da segunda bola, vamos começar pensando no movimento horizontal, este que é retilíneo e uniforme:\begin{matrix} x_f - x_i = (50 \cos{30º}) \Delta t &,& x_i = 0 &\therefore& x_f = 75\sqrt{3} \ \pu{m} \end{matrix}Já para a posição vertical:\begin{matrix} y_f - y_i = (50 \sin{30º})\Delta t + (-g)\dfrac{(\Delta t)^2}{2} &,& y_i = 0 \end{matrix}Assim,\begin{matrix} y_ f = 30 \ \pu{m} \end{matrix}Portanto, no plano cartesiano, a posição da bola é: $ (75\sqrt{3} , 30)$ $\color{#3368b8}{\text{Nota:}}$ Foram utilizadas as mesmas variáveis pois são análises distintas, não conferindo perda de generalidade. (Afinal, a ideia é apenas encontrar a posição de cada bola). Por fim, resta-nos aplicar a distância euclidiana e encontrar a distância $d$ solicitada:\begin{matrix} d = \sqrt{(75\sqrt{3} - 0)^2 + (30-45)^2} \end{matrix}\begin{matrix}\boxed{d = \sqrt{17100} \ \pu{m}} \end{matrix}\begin{matrix}Letra \ (C) \end{matrix}