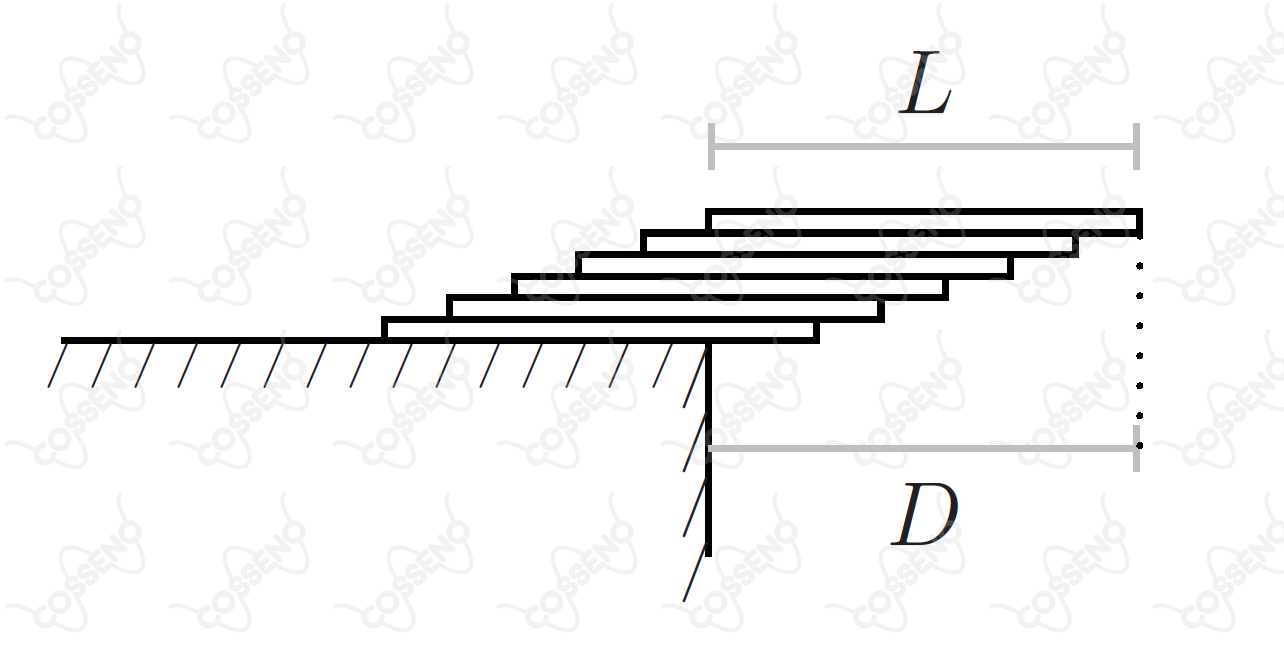
Chapas retangulares rígidas, iguais e homogêneas, são sobrepostas e deslocadas entre si, formando um conjunto que se apoia parcialmente na borda de uma calçada. A figura ilustra esse conjunto com chapas, bem como a distância alcançada pela sua parte suspensa. Desenvolva uma fórmula geral da máxima distância possível de modo que o conjunto ainda se mantenha em equilíbrio. A seguir, calcule essa distância em função do comprimento de cada chapa, para unidades.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

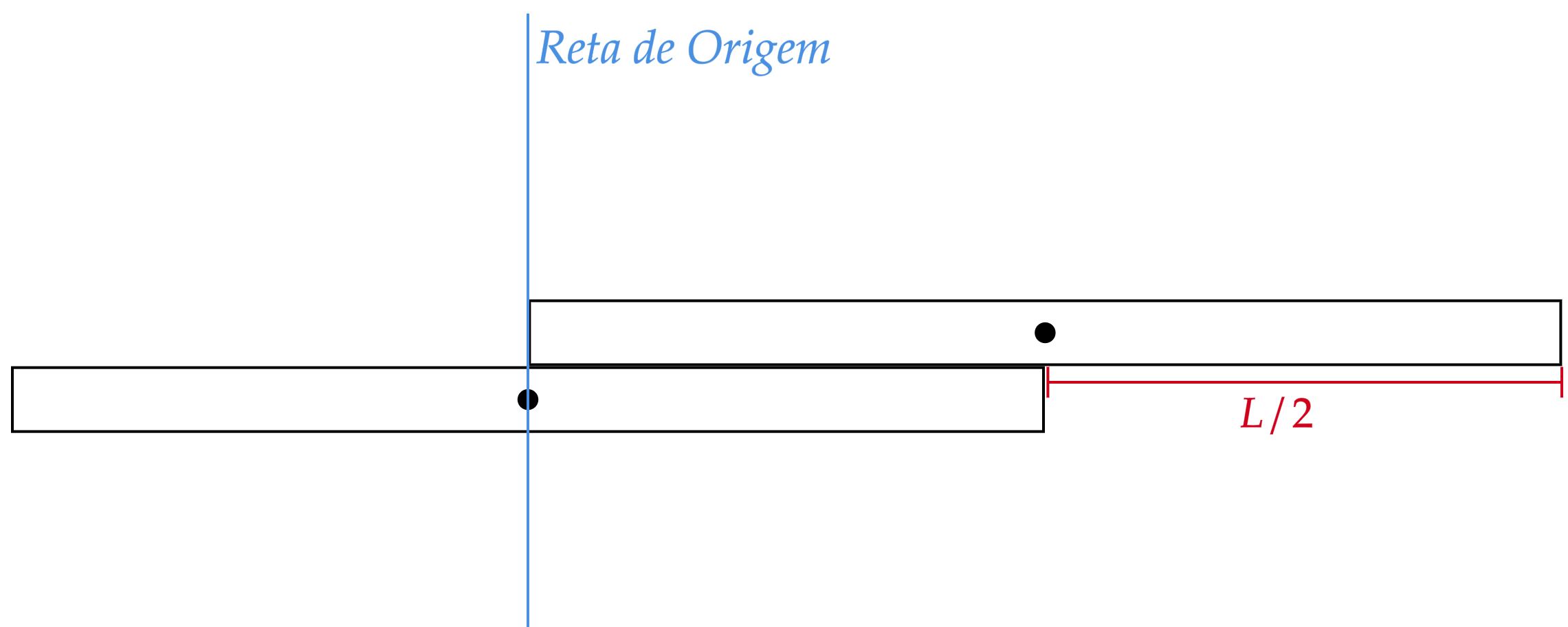
A princípio, vamos começar pensando a partir da última chapa sobreposta, pois, para não haver rotação, o centro de massa da chapa sucessora - ou composição de barras - deve estar acima da extremidade da barra antecessora (isso pensando na situação de distância máxima para $D$). Nesse contexto, podemos partir da análise simples de duas chapas, a ideia aqui é ver o que acontece e procurar uma recorrência. (Sabemos que há uma recorrência pelo simples fato da questão nos pedir para desenvolver uma fórmula.) Para duas chapas, têm-se:
 Bem, creio que não possamos tirar muita coisa disso, então vamos tentar com três barras. Nesse caso, iremos primeiro pensar na união das duas chapas em questão, e encontrar o centro de massa resultante, então:\begin{matrix}
x_{cm} = \dfrac{m(0) + m(L/2)}{m+m} = \dfrac{L}{4}
\end{matrix}Consequentemente, ao adicionar a terceira barra, têm-se:
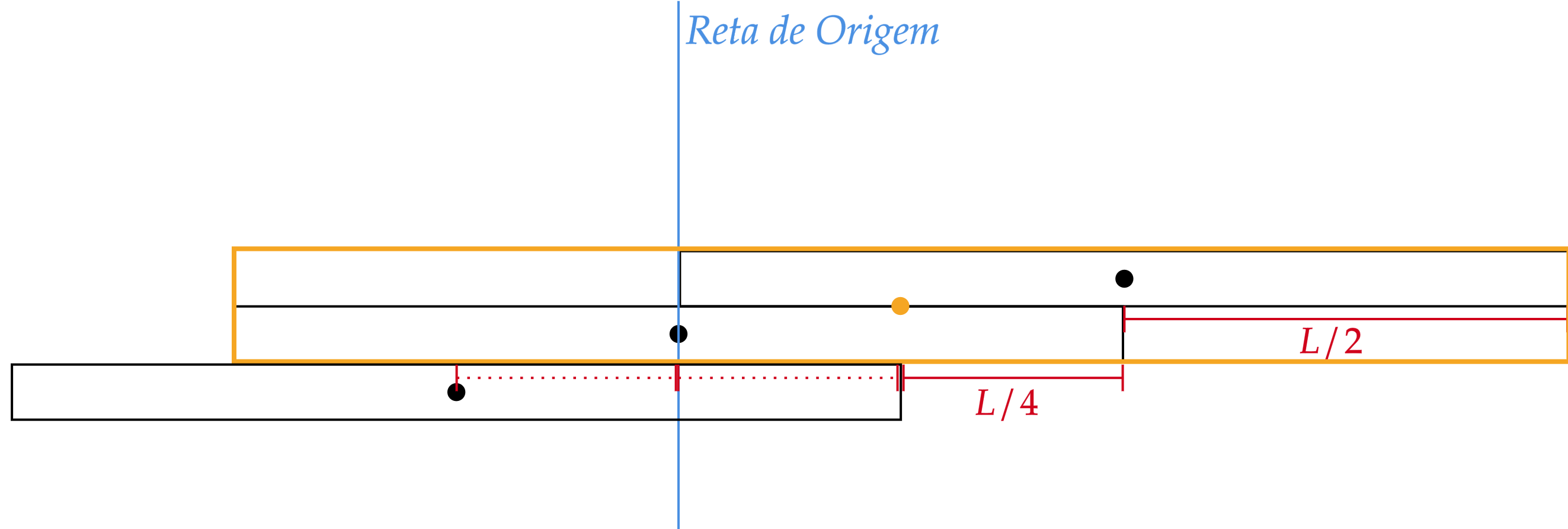
Bem, creio que não possamos tirar muita coisa disso, então vamos tentar com três barras. Nesse caso, iremos primeiro pensar na união das duas chapas em questão, e encontrar o centro de massa resultante, então:\begin{matrix}
x_{cm} = \dfrac{m(0) + m(L/2)}{m+m} = \dfrac{L}{4}
\end{matrix}Consequentemente, ao adicionar a terceira barra, têm-se:
 Agora, as coisas já estão ficando um pouco mais claras, mas vamos repetir o processo a fim de adicionar outra chapa:\begin{matrix}
x_{cm} = \dfrac{m(-L/4) + 2m(L/4)}{m+2m} = \dfrac{L}{12}
\end{matrix}Assim,
Agora, as coisas já estão ficando um pouco mais claras, mas vamos repetir o processo a fim de adicionar outra chapa:\begin{matrix}
x_{cm} = \dfrac{m(-L/4) + 2m(L/4)}{m+2m} = \dfrac{L}{12}
\end{matrix}Assim,
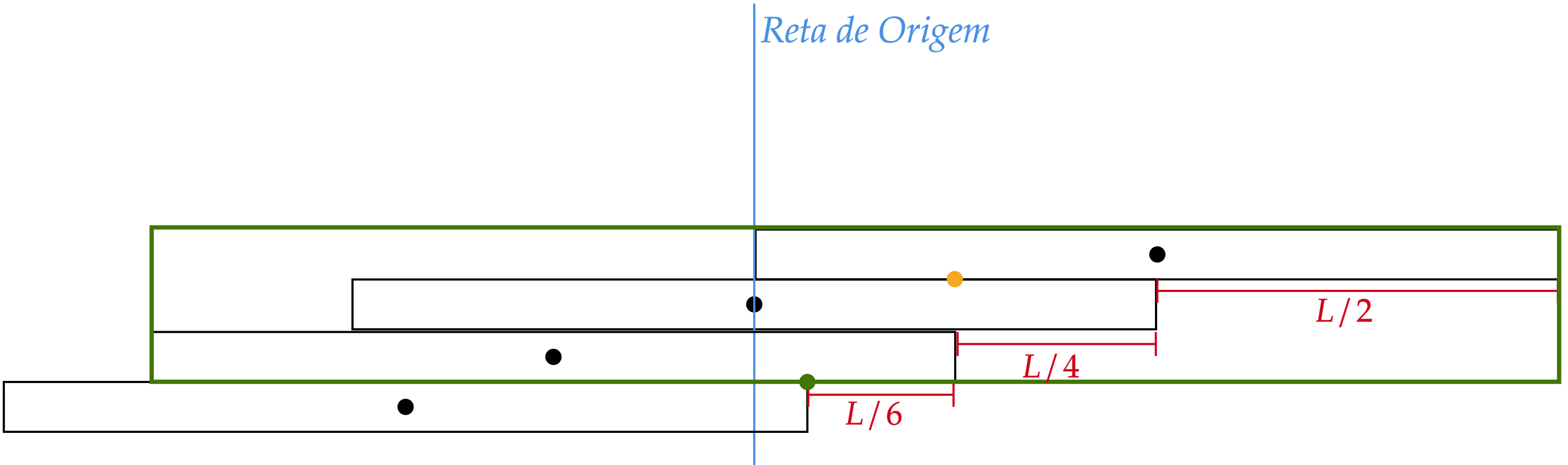 E aí está a nossa recorrência, veja que, por indução, deve-se ter:\begin{matrix} D &=& \dfrac{1}{1} \left( \dfrac{L}{2}\right) &+& \dfrac{1}{2} \left( \dfrac{L}{2}\right) &+& \dfrac{1}{3} \left( \dfrac{L}{2}\right) &+&...&+& \dfrac{1}{n} \left( \dfrac{L}{2}\right)
\end{matrix}Portanto, a fórmula geral deve ser:\begin{matrix}
\boxed{D_{(n)} = \left( \dfrac{L}{2}\right) \underset{i=1}{\overset{n}{\sum}} \dfrac{1}{i} }
\end{matrix}Ora, então para $n = 6$, concluímos:\begin{matrix}
D_{(6)} = \dfrac{147}{120}L &\therefore& \boxed{D_{(6)} = 1,225L}
\end{matrix}
E aí está a nossa recorrência, veja que, por indução, deve-se ter:\begin{matrix} D &=& \dfrac{1}{1} \left( \dfrac{L}{2}\right) &+& \dfrac{1}{2} \left( \dfrac{L}{2}\right) &+& \dfrac{1}{3} \left( \dfrac{L}{2}\right) &+&...&+& \dfrac{1}{n} \left( \dfrac{L}{2}\right)
\end{matrix}Portanto, a fórmula geral deve ser:\begin{matrix}
\boxed{D_{(n)} = \left( \dfrac{L}{2}\right) \underset{i=1}{\overset{n}{\sum}} \dfrac{1}{i} }
\end{matrix}Ora, então para $n = 6$, concluímos:\begin{matrix}
D_{(6)} = \dfrac{147}{120}L &\therefore& \boxed{D_{(6)} = 1,225L}
\end{matrix}

Ampliar Imagem

Ampliar Imagem

Ampliar Imagem

